7796: 学习系列 —— 图论 —— 有向图的强连通分量 II —— 缩点建新图
[Creator : ]
Description
在上一部分,我们学习了统计SCC,这仅仅是解题的第一步。
一般我们解题后面就是缩点建立新图,统计出入度。
下面我们来看一下为什么要缩点。我们有这样一个题目:
给你一张有向图,每个点都有一个点权(不是边权了哦),且每一个点都可以经过任意多次,但是点权只能加一次,求这张图的最大权值。
看上去很简单,也许你觉得只需要使用最短路径算法就可以完成。当时,如果图中有环(环就是一个 SCC),如下图所示的路径。
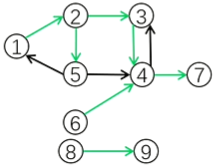
最短路算法就不能使用了,因此我们需要对上图进行缩点,变为下图。
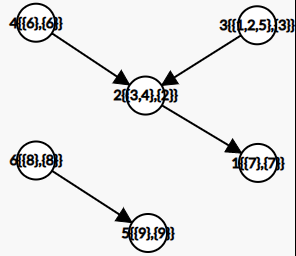
这样新的图就是一个 DAG(有向无环图),我们只需要进行一次拓扑排序即可。
特别注意:不是所有的题目都要建立新图的,只需要统计新图的出度和入度即可。
一般我们解题后面就是缩点建立新图,统计出入度。
【缩点】
根据强连通分量的定义,我们知道一个 SCC 内部所有点都是可以互相到达的,也就说我们可以将一个 SCC 看成一个点,这就是所谓的缩点。下面我们来看一下为什么要缩点。我们有这样一个题目:
给你一张有向图,每个点都有一个点权(不是边权了哦),且每一个点都可以经过任意多次,但是点权只能加一次,求这张图的最大权值。
看上去很简单,也许你觉得只需要使用最短路径算法就可以完成。当时,如果图中有环(环就是一个 SCC),如下图所示的路径。

最短路算法就不能使用了,因此我们需要对上图进行缩点,变为下图。

这样新的图就是一个 DAG(有向无环图),我们只需要进行一次拓扑排序即可。
特别注意:不是所有的题目都要建立新图的,只需要统计新图的出度和入度即可。
Input
【数据结构】
const int N=5e5+10;//根据题目要求定义 const int M=2*N;//注意一定要使用2倍,因为我们需要重新建图,最差情况就是每个点都是一个SCC //存图相关变量 LL h[N];//老图头结点 LL hn[N];//新图头结点 LL e[M], ne[M], idx;//存边 //SCC相关变量 LL dfn[N], low[N], ts;//时间戳 LL stk[N], top;//手写栈 bool instk[N];//结点是否在栈内 LL scc_cnt;//scc个数 LL scc[N];//编号为i的结点在哪个SCC LL sz[N];//编号为i的SCC内有几个结点 LL din[N];//新图结点入读 LL dout[N];//新图结点出度 //其实就是在原来的SCC基础上加入 din, dout。 //特别注意 M 的大小
【建图函数】
和老的 add() 函数有些差别,指定了建图的头结点数组。void add(LL a, LL b, LL h[]) {
//a->b 建到对应的 h[] 数组中
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
【缩点】
注意,不少题目需要在求 SCC 过程中,统计数据。比如统计 SCC 内最大结点编号,统计 SCC 内所有点权总和。
我们重新遍历图的所有边,利用 SCC 信息,重新建立新图。
//缩点
for (LL u=1; u<=n; u++) {
//顶点u的所有出边
for (LL i=h; i!=-1; i=ne[i]) {
LL v=e[i];
LL su=scc;//缩点后的u
LL sv=scc[v];//缩点后的v
if (su!=sv) {
//2->3 u=2 v=3
//u=2 -> su=scc=scc[2]=2
//v=3 -> sv=scc[v]=scc[3]=1
//su->sv 也就是缩点后 2->1
//统计出入度
din[sv]++;
dout[su]++;
//建立新图
add(su, sv, hn);
}
}
}
【后续处理】
一般就是对新图进行相应的算法处理。