6993: 「一本通 3.5 例 1」受欢迎的牛
[Creator : ]
Description
原题来自:USACO 2003 Fall
每一头牛的愿望就是变成一头最受欢迎的牛。现在有 N 头牛,给你 M 对整数 (A,B),表示牛 A 认为牛 B 受欢迎。这种关系是具有传递性的,如果 A 认为 B 受欢迎,B 认为 C 受欢迎,那么牛 A 也认为牛 C 受欢迎。你的任务是求出有多少头牛被除自己之外的所有牛认为是受欢迎的。
每一头牛的愿望就是变成一头最受欢迎的牛。现在有 N 头牛,给你 M 对整数 (A,B),表示牛 A 认为牛 B 受欢迎。这种关系是具有传递性的,如果 A 认为 B 受欢迎,B 认为 C 受欢迎,那么牛 A 也认为牛 C 受欢迎。你的任务是求出有多少头牛被除自己之外的所有牛认为是受欢迎的。
Input
第一行两个数 N,M;
接下来 M 行,每行两个数 A,B,意思是 A 认为 B 是受欢迎的(给出的信息有可能重复,即有可能出现多个 A,B)。
接下来 M 行,每行两个数 A,B,意思是 A 认为 B 是受欢迎的(给出的信息有可能重复,即有可能出现多个 A,B)。
Output
输出被除自己之外的所有牛认为是受欢迎的牛的数量。
Constraints
对于全部数据,$1\le N\le 10^4,1\le M\le 5\times 10^4$。
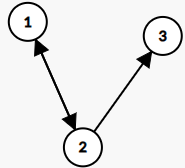
Sample 1 Input
3 3
1 2
2 1
2 3
Sample 1 Output
1
缩点后结构如下图

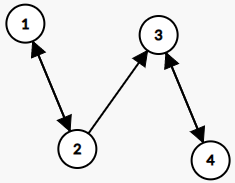
Sample 2 Input
4 5
1 2
2 1
2 3
3 4
4 3
Sample 2 Output
2
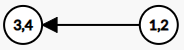
缩点后,结构如下图
Sample 3 Input
3 2
1 2
1 3
Sample 3 Output
0