7761: 学习系列 —— 图论 —— 有向图的强连通分量 I —— 统计SCC
[Creator : ]
Description
【概念】
1) 强连通图:有向图 $G$ 中,若对任意两点,从顶点 $V_i$ 到顶点 $V_j$,都存在从 $V_i$ 到 $V_j$ 以及从 $V_j$ 到 $V_i$ 的路径,则称 $G$ 是强连通图。2) 强连通分量:有向图 $G$ 的强连通子图称为 $G$ 的强连通分量。

图中,子图 $\{1,2,3,4\}$ 为一个强连通分量,因为顶点 $1,2,3,4$ 两两可达。$\{5\},\ \{6\}$ 也分别是两个强连通分量。
【Tarjan 算法】
【时间复杂度】
$O(n+m)$。【4 种边】
树边(tree edge):示意图中以黑色边表示,每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
反祖边(back edge):示意图中以红色边表示(即 $7 \to 1$),也被叫做回边,即指向祖先结点的边。
横叉边(cross edge):示意图中以蓝色边表示(即 $9 \to 7$),它主要是在搜索的时候遇到了一个已经访问过的结点,但是这个结点 并不是 当前结点的祖先。
前向边(forward edge):示意图中以绿色边表示(即 $3 \to 6$),它是在搜索的时候遇到子树中的结点的时候形成的。
【算法】
Tarjan 算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。
【定义】
DFN 为节点 $u$ 搜索的次序编号(时间戳)。Low 为 $u$ 或 $u$ 的子树能够追溯到的最早的栈中节点的次序号。
由定义可以得出,
Low=Min{Low, Low[v]},其中 $(u,v)$ 为树枝边,$u$ 为 $v$ 的父节点。
Low=Min{Low, DFN[v]},其中 $(u,v)$ 为指向栈中节点的后向边指向栈中结点的横叉边。
当结点 $u$ 搜索结束后,若 DFN=Low 时,则以 $u$ 为根的搜索子树上所有还在栈中的节点是一个强连通分量。
Input
【Tarjan 算法过程】
Tarjan算法需要维护两个数组:Dfn(节点被访问的时间,又叫时间戳),Low(回溯时能够回溯到最小的 Dfn 值)。1. 当首次遍历节点 $u$ 时,dfn = low ;
2. $u$ 入栈,更新 low;
3. 遍历与 $u$ 相邻的边 $(u, v)$,
若 $v$ 不在栈中,$u$ 是 $v$ 的父节点,low = min(low , low[v]);
若 $v$ 在栈中, low = min (low , dfn[v]);
4. 在 $u$ 的子树都遍历完了之后,若 low = dfn,则栈顶到 $u$ 之间(包括栈顶以及 $u$)的元素组成了一个强连通分量。
5. 继续搜索。
tarjan(u)
{
DFN=Low=++Index // 为节点u设定次序编号和Low初值
Stack.push(u) // 将节点u压入栈中
for each (u, v) in E // 枚举每一条边
if (v is not visted) // 如果节点v未被访问过
tarjan(v) // 继续向下找
Low = min(Low, Low[v])
else if (v in S) // 如果节点u还在栈内
Low = min(Low, DFN[v])
if (DFN == Low) // 如果节点u是强连通分量的根
repeat
v = S.pop // 将v退栈,为该强连通分量中一个顶点
print v
until (u== v)
}
Output
【模拟过程】
【初始状态】
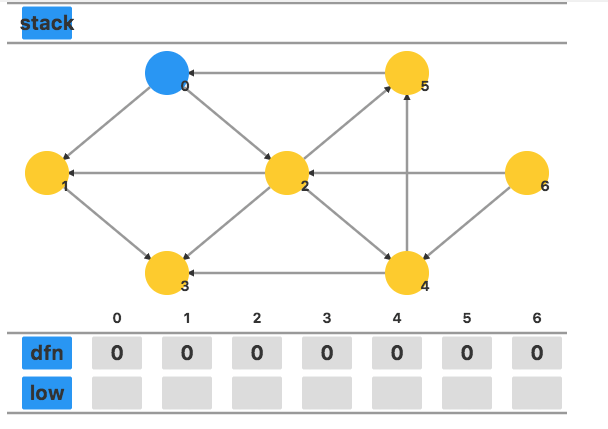
【模拟过程】
从 $0$ 开始 dfs。将顶点 $0$ 的 dfn[0] 和 low[0] 都设置为当前时间戳 $1$。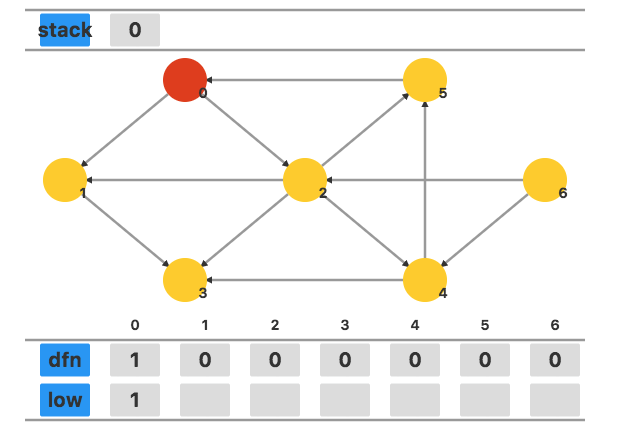
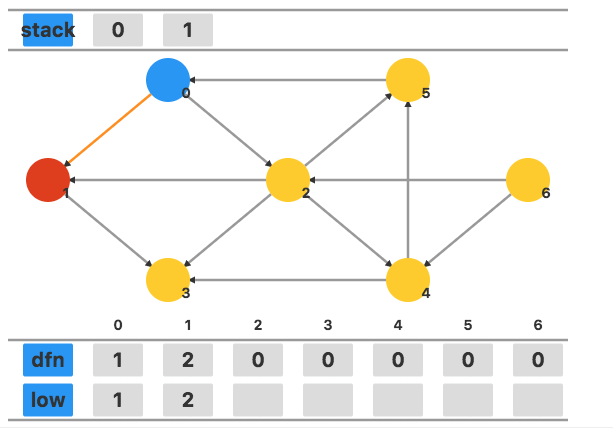
接下来访问相邻未访问的顶点 $1$,将 dfn[1] 和 low[1] 都设置为当前时间戳 $2$。
接下来访问相邻未访问顶点 $3$,将 dfn[3] 和 low[3] 都设置为当前时间戳 $3$。
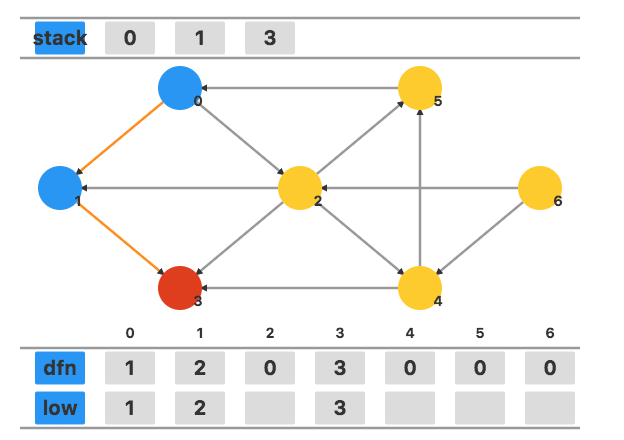
没有其他相邻顶点,此时 dfn[3]=low[3] ,故将 $3$ 出栈作为一个强连通分量。
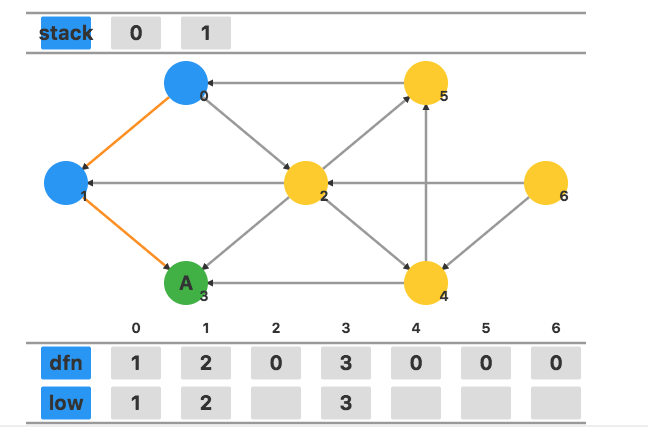
同样地,因为 dfn[1]=low[1],所以将 $1$ 出栈作为一个强连通分量。

继续访问和 $0$ 相邻的其他顶点 $2$,将 dfn[2] 和 low[2] 都设置为当前的时间戳 $4$。

访问相邻顶点 $4$,将 dfn[4] 和 low[4] 都设置为当前的时间戳 $5$。

访问相邻顶点 $5$,将 dfn[5] 和 low[5] 都设置为当前的时间戳 $6$。
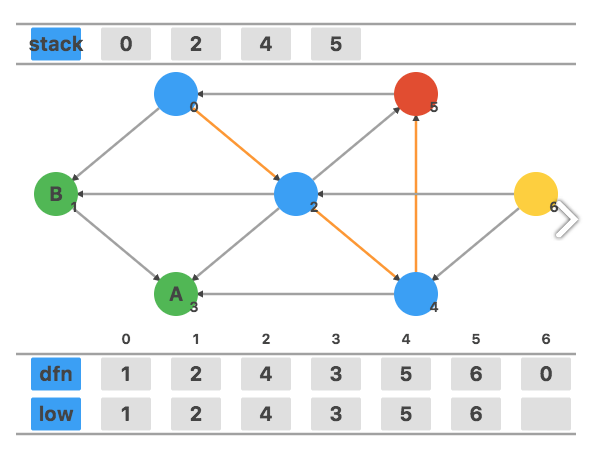
发现此时有指向栈中元素 $1$ 的边,将 low[5] 更新为 dfn[0]=1。
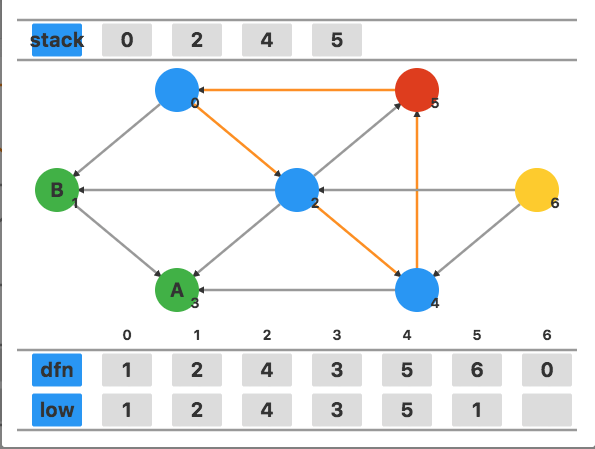
回溯到顶点 $4$,用 low[5] 更新 low[4],更新为 $1$。
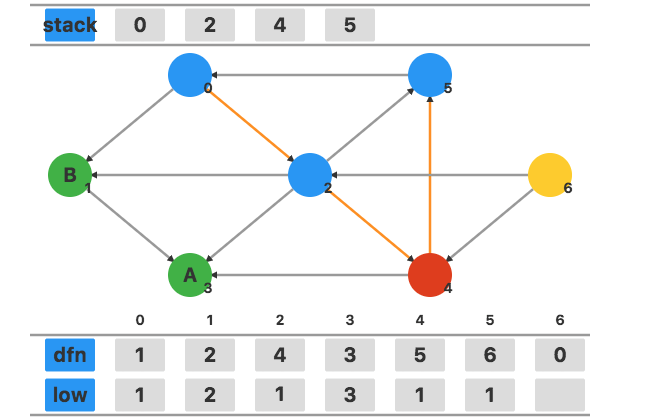
回溯到顶点 $2$,用 low[4] 更新 low[2],更新为 $1$。
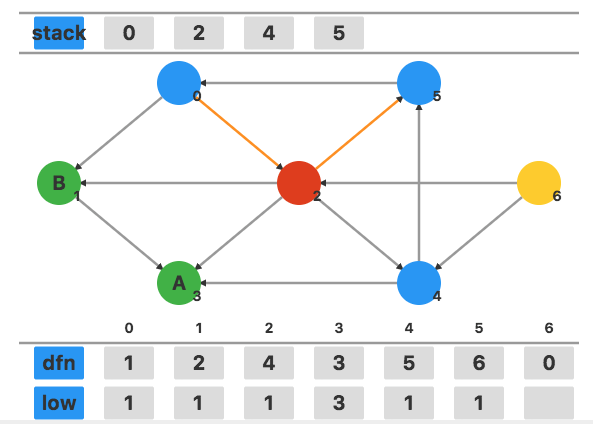
顶点 $2$ 有一个在栈中的相邻顶点 $5$,用 dfn[5] 更新 low[2],更新为 $2$,即不发生任何变化。
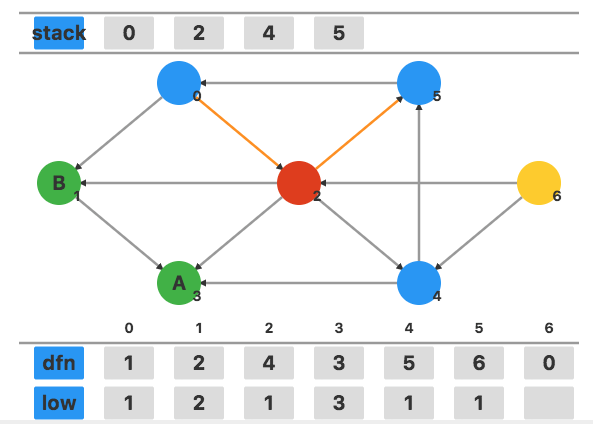
回溯到顶点 $0$,用 low[2] 更新 low[0]。此时发现 low[0]=dfn[0],将栈中元素弹出作为一个新的强连通分量。

找到下一个未访问的顶点 $6$,设置 dfn[6]=low[6]=7。
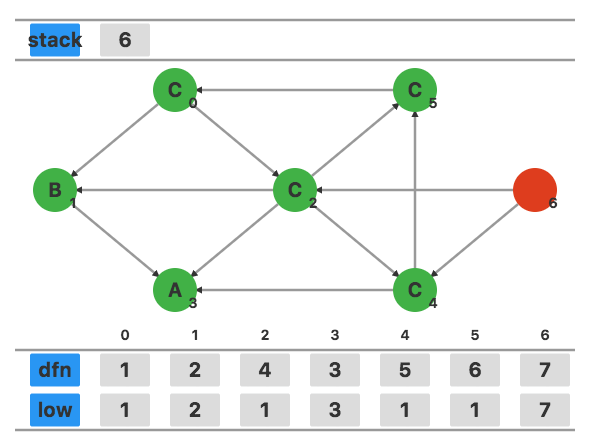
发现顶点 $6$ 没有指向栈中元素的边,搜索结束,将 $6$ 作为一个新的强连通分量。
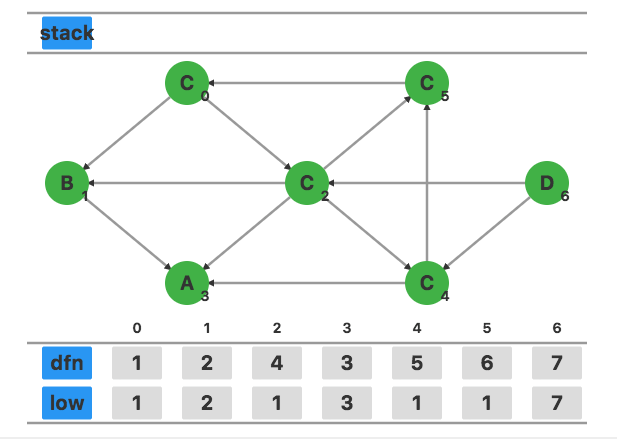
计算结束,$\{3\},\ \{1\},\ \{0,2,4,5\},\ \{6\}$ 是图中的四个强连通分量。
Constraints
【参考代码】
const int N=1e4+10;
LL h[N];
const int M=5e4+10;
LL e[M], ne[M], idx;
//tarjan相关
LL dfn[N];//时间戳
LL low[N];//时间戳
LL ts;//时间戳
LL scc[N];//编号为i的节点属于哪组强连通分量
LL siz[N];//编号为i的强连通分量组内节点数量
LL scc_cnt;//有cnt组强连通分量
//stack
LL stk[N], top;
bool instk[N];//编号为i的节点是否在栈中
//初始化
void init(LL n) {
idx=0;
scc_cnt=0;
ts=0;
for (LL i=0; i<=n; i++) {
h[i]=-1;
dfn[i]=low[i]=scc[i]=siz[i]=stk[i]=0;
instk[i]=false;
}
}
//加边函数
void add(LL a, LL b) {
//a->b
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
void tarjan(LL u) {
dfn[u]=low[u]=++ts;//记录时间戳
stk[++top]=u;//入栈
instk[u]=true;//u在栈里
//遍历u的所有出边
for (LL i=h[u]; i!=-1; i=ne[i]) {
LL v=e[i];
if (0==dfn[v]) {
//v点没有访问
tarjan(v);
//回u时,用low[v]更新low[u]
low[u]=min(low[u], low[v]);
} else if (true==instk[v]) {
//v已经访问,而且v在栈里
low[u]=min(low[u], dfn[v]);
}
}
//记录scc
if (dfn[u]==low[u]) {
//如果u是强连通分量
++scc_cnt;
//v到u是一组强连通分量
LL v;
do {
//弹栈
v=stk[top--];
instk[v]=false;
//加入到SCC
scc[v]=scc_cnt;//scc编号
++siz[scc_cnt];//scc大小
} while (v!=u);
}
}