6859: 学习系列 —— 动态规划 —— 数位 DP
[Creator : ]
Description
引入
数位 DP 往往都是这样的题型,给定一个闭区间 [l,r],让你求这个区间中满足某种条件的数的总数。而这个区间可能很大,简单的暴力代码如下:int ans=0;
for(int i=l;i<=r;i++){
if(check(i)) {
ans++;
}
}
若区间长度超过 $10^8$,我们暴力枚举就会超时了,而数位 DP 则可以解决这样的题型。数位 DP 实际上就是在数位上进行 DP。方法一:动态规划
数位
数位是指把一个数字按照个、十、百、千等等一位一位地拆开,关注它每一位上的数字。如果拆的是十进制数,那么每一位数字都是 0~9,其他进制可类比十进制。数位 DP:用来解决一类特定问题,这种问题比较好辨认,一般具有这几个特征:
-
要求统计满足一定条件的数的数量(即,最终目的为计数);
-
这些条件经过转化后可以使用「数位」的思想去理解和判断;
-
输入会提供一个数字区间(有时也只提供上界)来作为统计的限制;
-
上界很大(比如 $10^{18}$),暴力枚举验证会超时。
基本原理
考虑人类计数的方式,最朴素的计数就是从小到大开始依次加一。但我们发现对于位数比较多的数,这样的过程中有许多重复的部分。例如,从 $7000$ 数到 $7999$、从 $8000$ 数到 $8999$、和从 $9000$ 数到 $9999$ 的过程非常相似,它们都是后三位从 $000$ 变到 $999$,不一样的地方只有千位这一位,所以我们可以把这些过程归并起来,将这些过程中产生的计数答案也都存在一个通用的数组里。此数组根据题目具体要求设置状态,用递推或 DP 的方式进行状态转移。例如,我们对数字 $386$ 进行数位 DP,如下图所示。
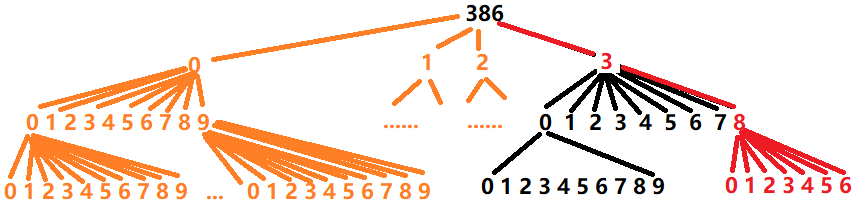
技巧
我们从最高位到最低位逐一处理。分类填数
设整数 $X$ 一共有 $n$ 位,那么 $X$ 可以表示为 $a_{n}a_{n-1}\dots a_{1}$,从高位到低位枚举填写。因为不含有前导零,所为最高位只能填写 $1 \sim a_{n}-1$,其他位可以填写 $0 \sim a_i$。如下图所示。
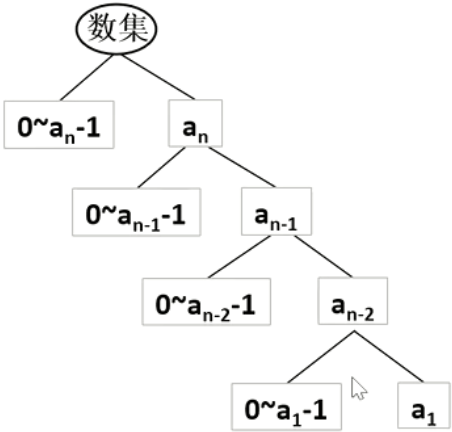

每个位上填数的时候,分为两类:$0 \sim a_i-1$ 和 $a_i$,这样填数可以保证不超过 $X$。
技巧 1
类似前缀和思想,转化问题为 [0,R] - [0, L-1] 求解。技巧 2
从高位到低位填数,要分类讨论。吧整数 R 的每一位抠出来,存入数组 a,则 $R=a_{n}a_{n-1}\dots a_{1}$。
如果 $i$ 位填写 $0 \sim a_i-1$,则后面每一位可以填 $0 \sim 9$。
如果 $i$ 位填写 $a_i$,则再讨论下一位。
这样,保证填的数不超过 $R$。
答案
答案在上图的最左边分支。如下图所示。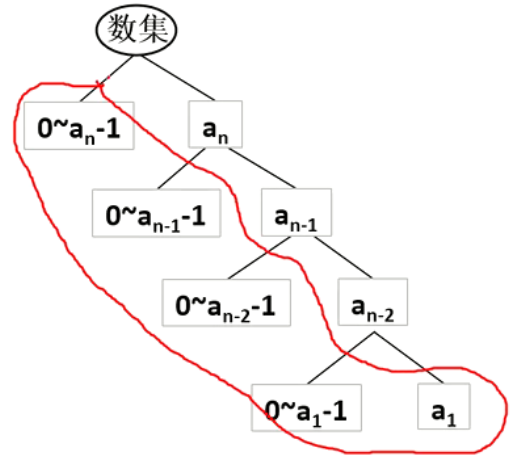
状态定义
定义 $f[i][j]$ 表示一共有 $i$ 位,且最高位数字为 $j$。预处理
由于我们是从高位向地位递推,所以需要预处理。void init() {
for (LL i=0; i<=9; i++) {//一位数
f[1][i]=1;
}
for (LL i=2; i<N; i++) {//阶段:枚举位数
for (LL j=0; j<=9; j++) {//状态:枚举最高位
for (LL k=j; k<=9; k++) {//决策:枚举次高位
f[i][j]+=f[i-1][k];//累加方案数
}
}
}
}
注意:每题的预处理都不一样,需要根据题目来确定。 预处理的时间复杂度为 $O(N*10*10)$,其中 $N$ 表示最大数据的位数。比如 $10^{18}$,那么就是 $N=18$。
所以预处理的时间是很短的。
Input
方法二:记忆化搜索
利用前缀和来求解答案 $\sum_{i=1}^{R}ans_i - \sum_{i=1}^{L−1} ans_i$。模板
int dfs(int pos, int pre, int lead, int limit) {
if (!pos) {
边界条件
}
if (!limit && !lead && dp[pos][pre] != -1) return dp[pos][pre];
int res = 0, up = limit ? a[pos] : 无限制位;
for (int i = 0; i <= up; i ++) {
if (不合法条件) continue;
res += dfs(pos - 1, 未定参数, lead && !i, limit && i == up);
}
return limit ? res : (lead ? res : dp[pos][sum] = res);
}
int cal(int x) {
memset(dp, -1, sizeof dp);
len = 0;
while (x) a[++ len] = x % 进制, x /= 进制;
return dfs(len, 未定参数, 1, 1);
}
signed main() {
cin >> l >> r;
cout << cal(r) - cal(l - 1) << endl;
}
cal 函数(一般情况):
注意每次初始化 DP 数组为 −1,长度 len=0基本参数
- len: 数位长度,一般根据这个来确定数组范围
- $a_i$: 每个数位具体数字
返回值
- 根据题目的初始条件来确定前导 0 以及 pre
DFS 函数(一般情况):
- 变量 res 来记录答案,初始化一般为 0
- 变量 up 表示能枚举的最高位数
if (!limit && !lead && dp[pos][pre] != -1) return dp[pos][pre]; 只有无限制、无前导零才算,不然都是未搜索完的情况。
return limit ? res : dp[pos][pre] = res; 如果最后还有限制,那么返回 res,否则返回 dp[pos][pre]
基本参数:
假设数字 $x$ 位数为 $a_1⋯a_n$必填参数:
- pos: 表示数字的位数
从末位或第一位开始,要根据题目的数字构造性质来选择顺序,一般选择从 $a_1$ 到 $a_n$ 的顺序。初始从 len 开始的话,边界条件应该是 pos=0,限制位数应该是 $a_{pos}$,DFS 时 pos−1;初始从1 开始的话,边界条件应该是 pos>len,限制位数应该是 $a_{len−pos+1}$,DFS 时 pos+1。两种都可以,看个人习惯。
- limit: 可以填数的限制(无限制的话 (limit=0) 0∼9 随便填,否则只能填到 $a_i$
如果搜索到 $a_1⋯a_{pos}⋯a_n$,原数位为 $a_1⋯a_k⋯a_n$,那么我们必须对接下来搜索的数加以限制,也就是不能超过区间右端点 R,所以要引入 limit 这个参数,如果 limit=1,那么最高位数 $up≤a_{pos+1}$,如果没有限制,那么 up=9(十进制下)这也就是确定搜索位数上界的语句 limit ? a[pos] : 9;
如果 limit=1 且已经取到了能取到的最高位时 $(a_{pos}=a_k)$,那么下一个 limit=1
如果 limit=1 且没有取到能取到的最高位时 $(a_{pos}<a_k)$,那么下一个 limit=0
如果 limit=0,那么下一个 limit=0,因为前一位没有限制后一位必定没有限制。
所以我们可以把这 3 种情况合成一个语句进行下一次搜索:limit && i == up ($i$ 为当前枚举的数字)
可选参数:
pre: 表示上一个数是多少有些题目会用到前面的数
lead: 前导零是否存在,lead=1 存在前导零,否则不存在。
一般来说有些题目不加限制前导零会影响数字结构,所以 lead 是一个很重要的参数。
如果 lead=1 且当前位为 0,那么说明当前位是前导 0,继续搜索 pos+1,其他条件不变。
如果 lead=1 且当前位不为 0,那么说明当前位是最高位,继续搜索 pos+1,条件变动。
如果 lead=0,则不需要操作。
sum: 搜索到当前所有数字之和
有些题目会出现数字之和的条件
cnt: 某个数字出现的次数
有些题目会出现某个数字出现次数的条件
参数基本的差不多这些,有些较难题目会用到更多方法或改变 DP。