基环树（pseudotree）

就是一个 $n$ 个点 $n$ 条边的连通图。简单来说，就是一个树加上了一条边形成了一个环。

所以基环树上的问题大多数都是先处理以环上的点为根节点的子树的值，然后在环上做 dp 之类的东西

无向基环树

找环

给定一个图，$N$ 个点 $N$ 条边，只有一个环，输出环上的点。
题目：MYOJ10394，洛谷P4318。

DFS找环

使用 DFS 搜索来找

并查集找环

拓扑排序找环

有向基环树

内向基环树

每个节点以自己为起点的边只有一条。如图

MYOJ10395, MYOJ10396.

外向树

每个节点以自己为终点的边只有一条。如图。

一般处理思路

以无向图为例子。

1. 大体方法

一般方法的：

1. 找到唯一的环；
2. 对环之外的部分按照若干棵树处理；
3. 考虑与环一起计算。

2. 找环

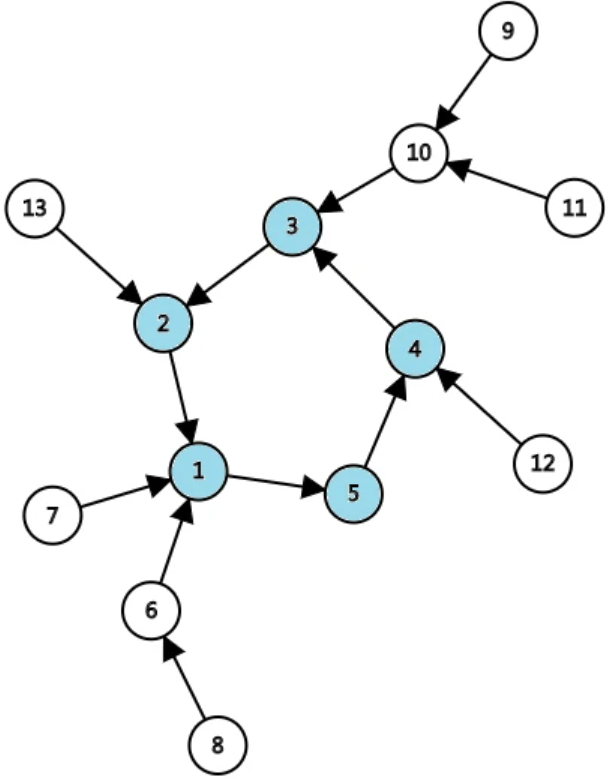
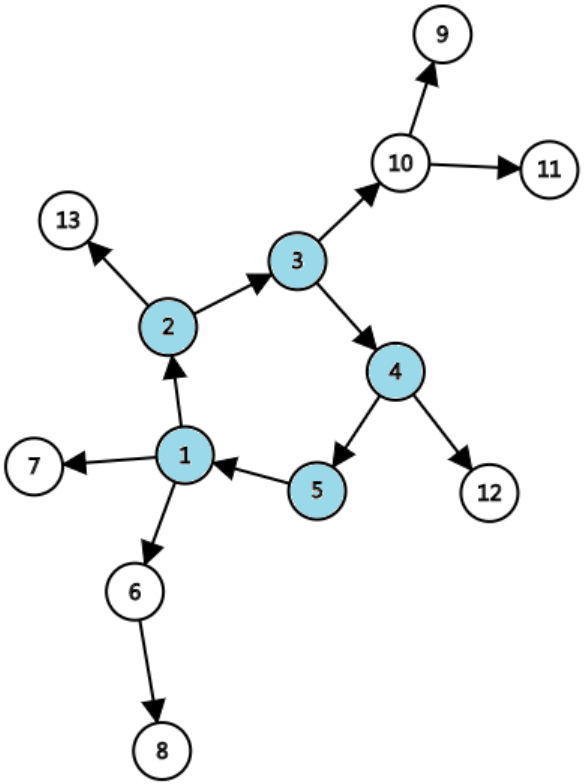
可以是DFS，并查集，拓扑排序。下面我们用一个动画来演示DFS找环的过程。

1. 从任意一点开始搜索；
2. 每次拓展到的点涂为灰色，回溯的点涂为黑色；
3. 重复第一、二步，直到通过一条未经过过的边拓展到一个灰色节点；
4. 将拓展到的灰色节点涂为红色，函数返回 true；
5. 将经过的回溯时经过的节点涂为橙色，函数返回 true；
6. 重复第 5. 步，直到回溯到被涂为红色的节点，函数返回 false，算法结束。

经过以上几步，我们便得到了唯一的环——颜色最显眼的那些！其中红色节点是环的衔接处。

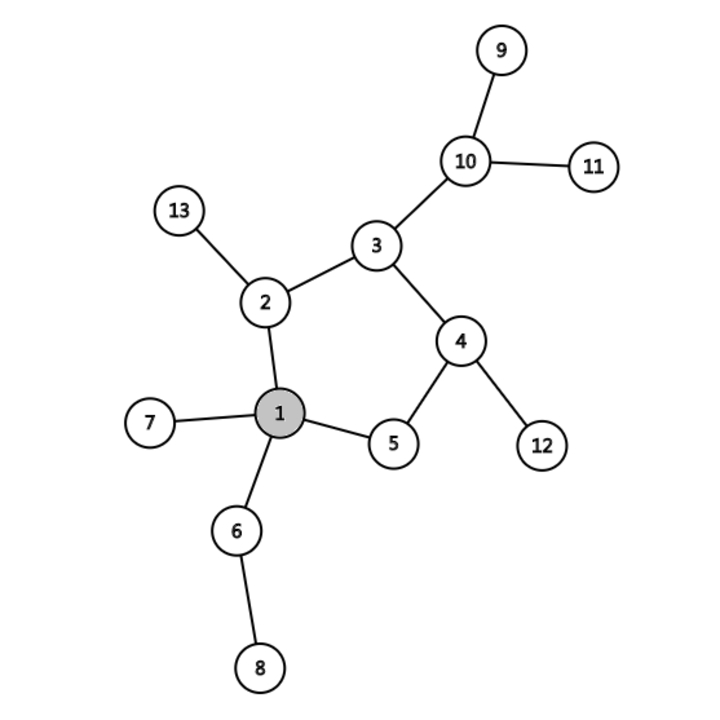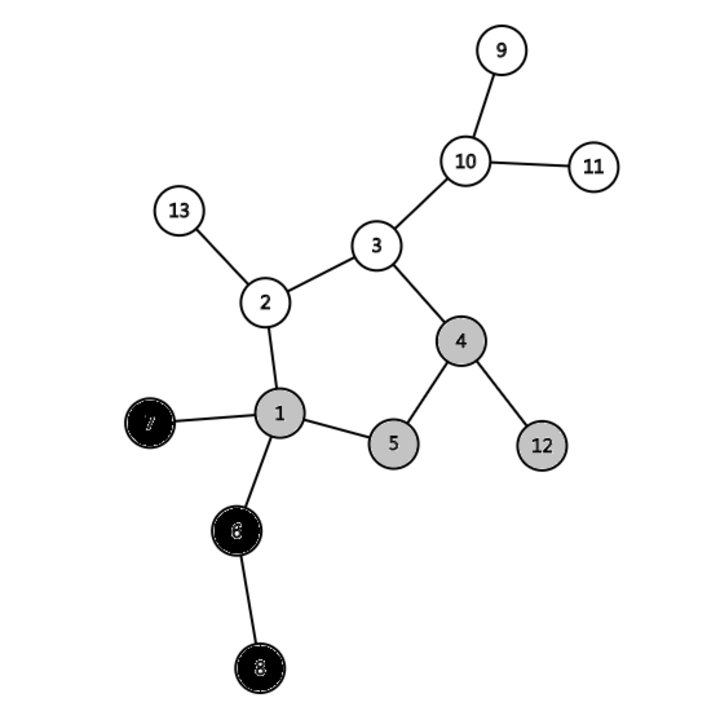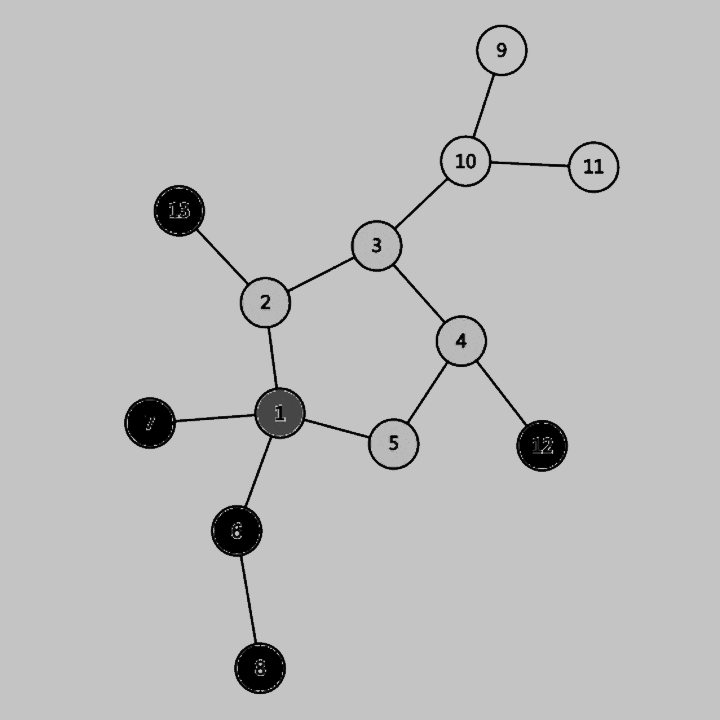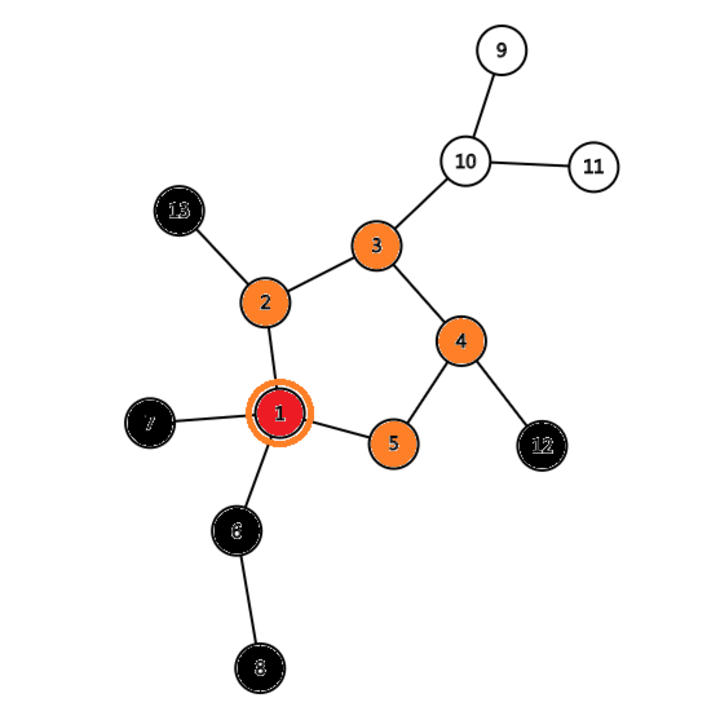
注意到，上面的模拟过程中，以节点 10 为根的子树并没有被遍历，是因为 DFS 的实现本身便是一路到底，所以可能并不能遍历整颗基环树。

3. 剩下操作

剩下的两步多要视题目而定了，不过一般是一个树形DP（子树不考虑环）加一个线性DP+单调队列优化（在环上，断环为链，复制一遍）