9987: ABC319 —— D - Minimum Width
[Creator : ]
Description
Takahashi is displaying a sentence with $N$ words in a window. All words have the same height, and the width of the $i$-th word $(1\leq i\leq N)$ is $L _ i$.
The words are displayed in the window separated by a space of width $1$. More precisely, when the sentence is displayed in a window of width $W$, the following conditions are satisfied.
- The sentence is divided into several lines.
- The first word is displayed at the beginning of the top line.
- The $i$-th word $(2\leq i\leq N)$ is displayed either with a gap of $1$ after the $(i-1)$-th word, or at the beginning of the line below the line containing the $(i-1)$-th word. It will not be displayed anywhere else.
- The width of each line does not exceed $W$. Here, the width of a line refers to the distance from the left end of the leftmost word to the right end of the rightmost word.
When Takahashi displayed the sentence in the window, the sentence fit into $M$ or fewer lines. Find the minimum possible width of the window.
The words are displayed in the window separated by a space of width $1$. More precisely, when the sentence is displayed in a window of width $W$, the following conditions are satisfied.
- The sentence is divided into several lines.
- The first word is displayed at the beginning of the top line.
- The $i$-th word $(2\leq i\leq N)$ is displayed either with a gap of $1$ after the $(i-1)$-th word, or at the beginning of the line below the line containing the $(i-1)$-th word. It will not be displayed anywhere else.
- The width of each line does not exceed $W$. Here, the width of a line refers to the distance from the left end of the leftmost word to the right end of the rightmost word.
When Takahashi displayed the sentence in the window, the sentence fit into $M$ or fewer lines. Find the minimum possible width of the window.
Input
The input is given from Standard Input in the following format:
```
$N$ $M$
$L _ 1$ $L _ 2$ $\ldots$ $L _ N$
```
```
$N$ $M$
$L _ 1$ $L _ 2$ $\ldots$ $L _ N$
```
Output
Print the answer in one line.
Constraints
- $1\leq M\leq N\leq2\times10 ^ 5$
- $1\leq L _ i\leq10^9\ (1\leq i\leq N)$
- All input values are integers.
- $1\leq L _ i\leq10^9\ (1\leq i\leq N)$
- All input values are integers.
Sample 1 Input
13 3
9 5 2 7 1 8 8 2 1 5 2 3 6
Sample 1 Output
26
When the width of the window is 26, you can fit the given sentence into three lines as follows.
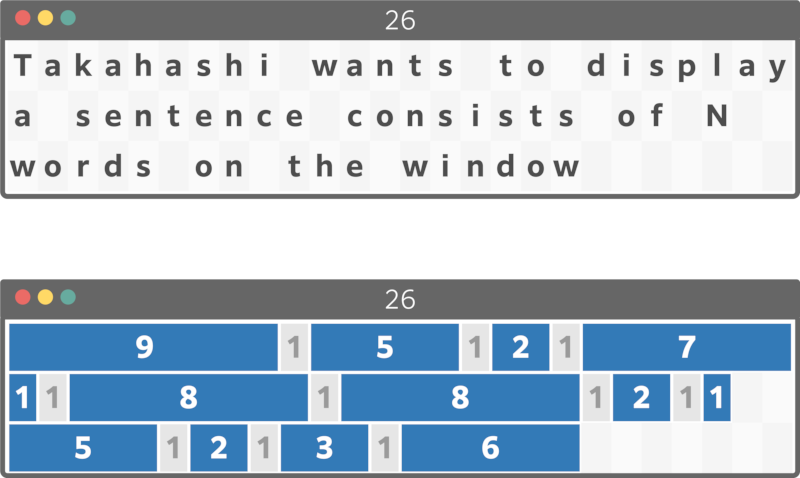
You cannot fit the given sentence into three lines when the width of the window is 25 or less, so print 26.
Note that you should not display a word across multiple lines, let the width of a line exceed the width of the window, or rearrange the words.

You cannot fit the given sentence into three lines when the width of the window is 25 or less, so print 26.
Note that you should not display a word across multiple lines, let the width of a line exceed the width of the window, or rearrange the words.

Sample 2 Input
10 1
1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
Sample 2 Output
10000000009
Note that the answer may not fit into a 32bit integer.
Sample 3 Input
30 8
8 55 26 97 48 37 47 35 55 5 17 62 2 60 23 99 73 34 75 7 46 82 84 29 41 32 31 52 32 60
Sample 3 Output
189