9986: ABC319 —— C - False Hope
[Creator : ]
Description
There is a $3\times3$ grid with numbers between $1$ and $9$, inclusive, written in each square. The square at the $i$-th row from the top and $j$-th column from the left $(1\leq i\leq3,1\leq j\leq3)$ contains the number $c _ {i,j}$.
The same number may be written in different squares, but not in three consecutive cells vertically, horizontally, or diagonally. More precisely, it is guaranteed that $c _ {i,j}$ satisfies all of the following conditions.
- $c _ {i,1}=c _ {i,2}=c _ {i,3}$ does not hold for any $1\leq i\leq3$.
- $c _ {1,j}=c _ {2,j}=c _ {3,j}$ does not hold for any $1\leq j\leq3$.
- $c _ {1,1}=c _ {2,2}=c _ {3,3}$ does not hold.
- $c _ {3,1}=c _ {2,2}=c _ {1,3}$ does not hold.
Takahashi will see the numbers written in each cell in random order. He will get disappointed when there is a line (vertical, horizontal, or diagonal) that satisfies the following condition.
- The first two squares he sees contain the same number, but the last square contains a different number.
Find the probability that Takahashi sees the numbers in all the squares without getting disappointed.
The same number may be written in different squares, but not in three consecutive cells vertically, horizontally, or diagonally. More precisely, it is guaranteed that $c _ {i,j}$ satisfies all of the following conditions.
- $c _ {i,1}=c _ {i,2}=c _ {i,3}$ does not hold for any $1\leq i\leq3$.
- $c _ {1,j}=c _ {2,j}=c _ {3,j}$ does not hold for any $1\leq j\leq3$.
- $c _ {1,1}=c _ {2,2}=c _ {3,3}$ does not hold.
- $c _ {3,1}=c _ {2,2}=c _ {1,3}$ does not hold.
Takahashi will see the numbers written in each cell in random order. He will get disappointed when there is a line (vertical, horizontal, or diagonal) that satisfies the following condition.
- The first two squares he sees contain the same number, but the last square contains a different number.
Find the probability that Takahashi sees the numbers in all the squares without getting disappointed.
Input
The input is given from Standard Input in the following format:
```
$c _ {1,1}$ $c _ {1,2}$ $c _ {1,3}$
$c _ {2,1}$ $c _ {2,2}$ $c _ {2,3}$
$c _ {3,1}$ $c _ {3,2}$ $c _ {3,3}$
```
```
$c _ {1,1}$ $c _ {1,2}$ $c _ {1,3}$
$c _ {2,1}$ $c _ {2,2}$ $c _ {2,3}$
$c _ {3,1}$ $c _ {3,2}$ $c _ {3,3}$
```
Output
Print one line containing the probability that Takahashi sees the numbers in all the squares without getting disappointed. Your answer will be considered correct if the absolute error from the true value is at most $10 ^ {-8}$.
Constraints
- $c _ {i,j}\in\lbrace1,2,3,4,5,6,7,8,9\rbrace\ (1\leq i\leq3,1\leq j\leq3)$
- $c _ {i,1}=c _ {i,2}=c _ {i,3}$ does not hold for any $1\leq i\leq3$.
- $c _ {1,j}=c _ {2,j}=c _ {3,j}$ does not hold for any $1\leq j\leq3$.
- $c _ {1,1}=c _ {2,2}=c _ {3,3}$ does not hold.
- $c _ {3,1}=c _ {2,2}=c _ {1,3}$ does not hold.
- $c _ {i,1}=c _ {i,2}=c _ {i,3}$ does not hold for any $1\leq i\leq3$.
- $c _ {1,j}=c _ {2,j}=c _ {3,j}$ does not hold for any $1\leq j\leq3$.
- $c _ {1,1}=c _ {2,2}=c _ {3,3}$ does not hold.
- $c _ {3,1}=c _ {2,2}=c _ {1,3}$ does not hold.
Sample 1 Input
3 1 9
2 5 6
2 7 1
Sample 1 Output
0.666666666666666666666666666667
For example, if Takahashi sees $c_{3,1}=2,\ c_{2,1}=2,\ c_{1,1}=3$ in this order, he will get disappointed.
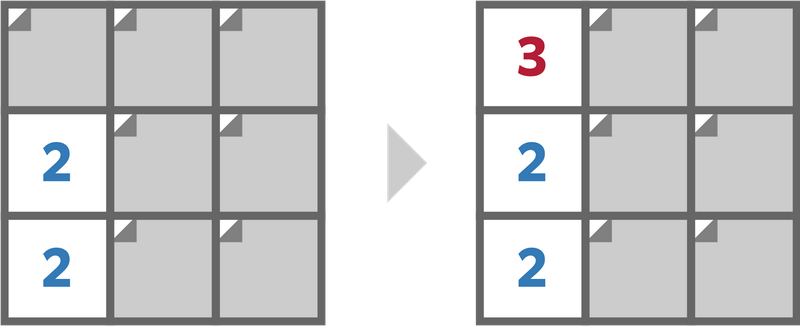
On the other hand, if Takahashi sees $c_{1,1},c_{1,2},c_{1,3},c_{2,1},c_{2,2},c_{2,3},c_{3,1},c_{3,2},c_{3,3}$ in this order, he will see all numbers without getting disappointed.
The probability that Takahashi sees all the numbers without getting disappointed is $\frac{2}{3}$. Your answer will be considered correct if the absolute error from the true value is at most $10^{-8}$, so outputs such as 0.666666657 and 0.666666676 would also be accepted.

On the other hand, if Takahashi sees $c_{1,1},c_{1,2},c_{1,3},c_{2,1},c_{2,2},c_{2,3},c_{3,1},c_{3,2},c_{3,3}$ in this order, he will see all numbers without getting disappointed.
The probability that Takahashi sees all the numbers without getting disappointed is $\frac{2}{3}$. Your answer will be considered correct if the absolute error from the true value is at most $10^{-8}$, so outputs such as 0.666666657 and 0.666666676 would also be accepted.
Sample 2 Input
7 7 6
8 6 8
7 7 6
Sample 2 Output
0.004982363315696649029982363316
Sample 3 Input
3 6 7
1 9 7
5 7 5
Sample 3 Output
0.4