9960: ABC314 —— Ex - Disk and Segments
[Creator : ]
Description
There are $N$ line segments in a coordinate plane, and the $i$\-th line segment $(1\leq i\leq N)$ has two points $(a _ i,b _ i)$ and $(c _ i,d _ i)$ as its endpoints. Here, each line segment includes its endpoints. Additionally, no two line segments share a point.
We want to place a single closed disk in this plane so that it shares a point with each line segment. In other words, we want to draw a single circle so that each line segment shares a point with either the circumference of the circle or its interior (or both). Find the smallest possible radius of such a disk.
We want to place a single closed disk in this plane so that it shares a point with each line segment. In other words, we want to draw a single circle so that each line segment shares a point with either the circumference of the circle or its interior (or both). Find the smallest possible radius of such a disk.
Input
The input is given from Standard Input in the following format:
```
$N$
$a _ 1$ $b _ 1$ $c _ 1$ $d _ 1$
$a _ 2$ $b _ 2$ $c _ 2$ $d _ 2$
$\vdots$
$a _ N$ $b _ N$ $c _ N$ $d _ N$
```
```
$N$
$a _ 1$ $b _ 1$ $c _ 1$ $d _ 1$
$a _ 2$ $b _ 2$ $c _ 2$ $d _ 2$
$\vdots$
$a _ N$ $b _ N$ $c _ N$ $d _ N$
```
Output
Print the answer in a single line. Your output will be considered correct when the absolute or relative error from the true value is at most $10 ^ {−5}$.
Constraints
- $2\leq N\leq 100$
- $0\leq a _ i,b _ i,c _ i,d _ i\leq1000\ (1\leq i\leq N)$
- $(a _ i,b _ i)\neq(c _ i,d _ i)\ (1\leq i\leq N)$
- The $i$-th and $j$-th line segments do not share a point $(1\leq i\lt j\leq N)$.
- All input values are integers.
- $0\leq a _ i,b _ i,c _ i,d _ i\leq1000\ (1\leq i\leq N)$
- $(a _ i,b _ i)\neq(c _ i,d _ i)\ (1\leq i\leq N)$
- The $i$-th and $j$-th line segments do not share a point $(1\leq i\lt j\leq N)$.
- All input values are integers.
Sample 1 Input
4
2 3 2 10
4 0 12 6
4 8 6 3
7 8 10 8
Sample 1 Output
3.319048676309097923796460081961
The given line segments are shown in the figure below. The closed disk shown in the figure, centered at $(\frac{32−\sqrt{115}}{4},\frac{21−\sqrt{115}}{2})$ with a radius of $\frac{24−\sqrt{115}}{4}$, shares a point with all the line segments.
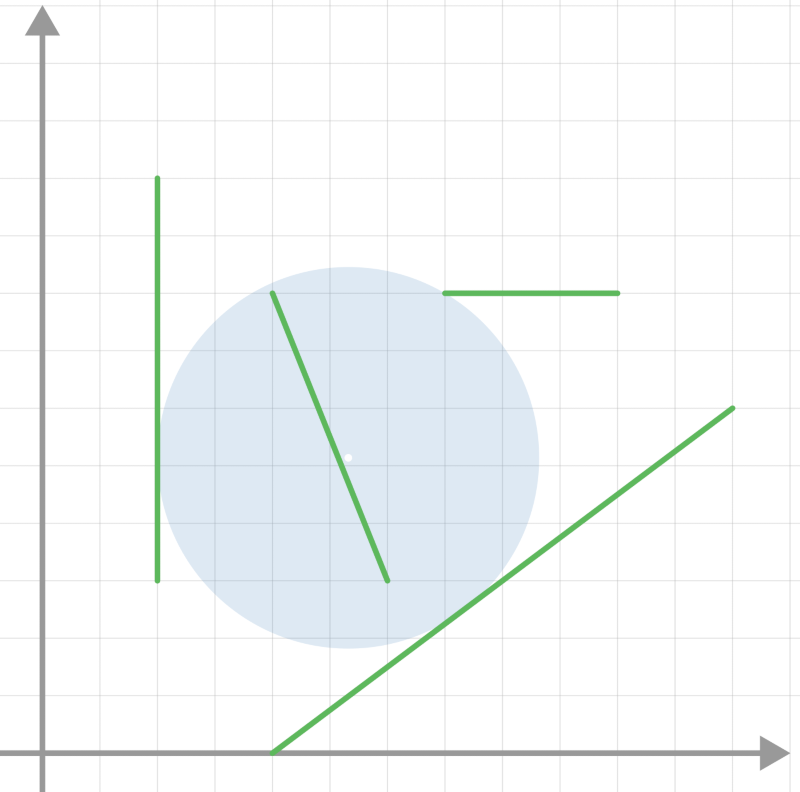
It is impossible to place a disk with a radius less than $\frac{24−\sqrt{115}}{4}$ so that it shares a point with all the line segments, so the answer is $\frac{24−\sqrt{115}}{4}$.
Your output will be considered correct if the absolute or relative error from the true value is at most $10^{-5}$, so outputs such as 3.31908 and 3.31902 would also be considered correct.

It is impossible to place a disk with a radius less than $\frac{24−\sqrt{115}}{4}$ so that it shares a point with all the line segments, so the answer is $\frac{24−\sqrt{115}}{4}$.
Your output will be considered correct if the absolute or relative error from the true value is at most $10^{-5}$, so outputs such as 3.31908 and 3.31902 would also be considered correct.
Sample 2 Input
20
0 18 4 28
2 21 8 21
3 4 10 5
3 14 10 13
5 9 10 12
6 9 10 6
6 28 10 18
12 11 15 13
12 17 12 27
13 17 20 18
13 27 19 26
16 1 16 13
16 22 19 25
17 22 20 19
18 4 23 4
18 5 23 11
22 16 22 23
23 15 30 15
23 24 30 24
24 0 24 11
Sample 2 Output
12.875165712523887403637822024952
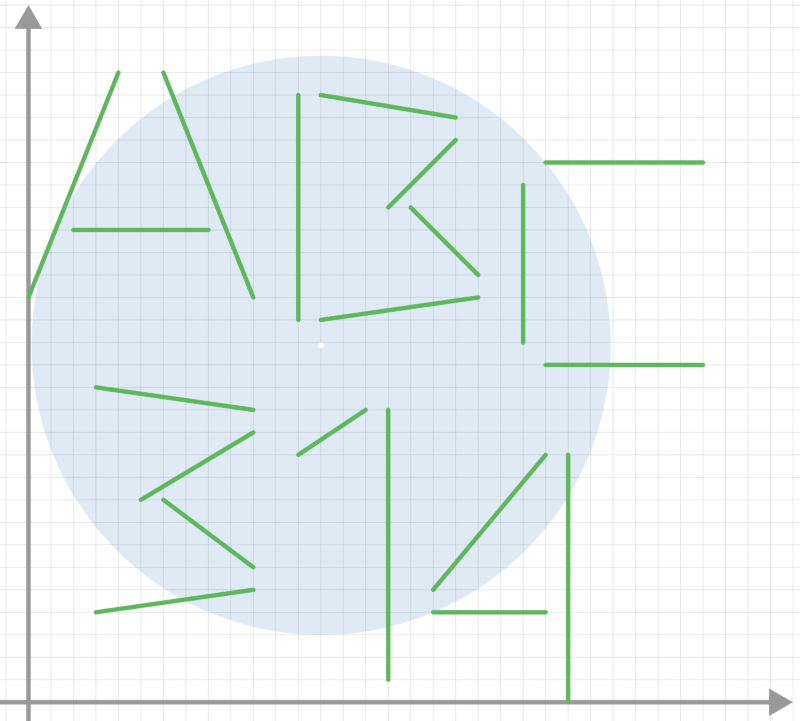
The closed disk shown in the figure, centered at $(\frac{19817−8\sqrt{5991922}}{18},\frac{−2305+\sqrt{5991922}}{9})$ with a radius of $\frac{3757\sqrt{29}−44\sqrt{206618}}{18}$, shares a point with all the line segments.

Sample 3 Input
30
526 655 528 593
628 328 957 211
480 758 680 794
940 822 657 949
127 23 250 385
281 406 319 305
277 598 190 439
437 450 725 254
970 478 369 466
421 225 348 141
872 64 600 9
634 460 759 337
878 514 447 534
142 237 191 269
983 34 554 284
694 160 589 239
391 631 22 743
377 656 500 606
390 576 184 312
556 707 457 699
796 870 186 773
12 803 505 586
343 541 42 165
478 340 176 2
39 618 6 651
753 883 47 833
551 593 873 672
983 729 338 747
721 77 541 255
0 32 98 597
Sample 3 Output
485.264732620930836460637042310401