9936: ABC311 —— Ex - Many Illumination Plans
[Creator : ]
Description
There is a rooted tree $T$ with $N$ vertices numbered $1$ to $N$. The root is vertex $1$, and the parent of vertex $i$ $(2 \leq i \leq N)$ is $P_i$.
Each vertex has two non-negative integer values called beauty and weight. The beauty and weight of vertex $i$ are $B_i$ and $W_i$, respectively.
Additionally, each vertex is painted red or blue. The color of vertex $i$ is represented by an integer $C_i$: vertex $i$ is painted red if $C_i = 0$, and blue if $C_i = 1$.
For vertex $v$, let $F(v)$ be the answer to the following problem.
> Let $U$ be the rooted tree that is the subtree of $T$ rooted at $v$.
> You can perform the following sequence of operations on $U$ zero or more times. (The operations do not affect the beauties, weights, or colors of the vertices that are not being deleted.)
>
> - Choose a vertex $c$ other than the root. Let $p$ be the parent of $c$.
> - For each edge whose endpoint on the parent side is $c$, do the following:
> - Let $u$ be the endpoint of the edge other than $c$. Delete the edge and connect $p$ and $u$ with a new edge, with $p$ on the parent side.
> - Delete the vertex $c$, and the edge connecting $p$ and $c$.
>
> A rooted tree that can be obtained as $U$ after some operations is called a good rooted tree when all of the following conditions are satisfied.
>
> - For every edge in $U$, the edge's endpoints have different colors.
> - The vertices have a total weight of at most $X$.
>
> Find the maximum possible total beauty of the vertices in a good rooted tree.
Find all of $F(1), F(2), \dots, F(N)$.
Each vertex has two non-negative integer values called beauty and weight. The beauty and weight of vertex $i$ are $B_i$ and $W_i$, respectively.
Additionally, each vertex is painted red or blue. The color of vertex $i$ is represented by an integer $C_i$: vertex $i$ is painted red if $C_i = 0$, and blue if $C_i = 1$.
For vertex $v$, let $F(v)$ be the answer to the following problem.
> Let $U$ be the rooted tree that is the subtree of $T$ rooted at $v$.
> You can perform the following sequence of operations on $U$ zero or more times. (The operations do not affect the beauties, weights, or colors of the vertices that are not being deleted.)
>
> - Choose a vertex $c$ other than the root. Let $p$ be the parent of $c$.
> - For each edge whose endpoint on the parent side is $c$, do the following:
> - Let $u$ be the endpoint of the edge other than $c$. Delete the edge and connect $p$ and $u$ with a new edge, with $p$ on the parent side.
> - Delete the vertex $c$, and the edge connecting $p$ and $c$.
>
> A rooted tree that can be obtained as $U$ after some operations is called a good rooted tree when all of the following conditions are satisfied.
>
> - For every edge in $U$, the edge's endpoints have different colors.
> - The vertices have a total weight of at most $X$.
>
> Find the maximum possible total beauty of the vertices in a good rooted tree.
Find all of $F(1), F(2), \dots, F(N)$.
Input
The input is given from Standard Input in the following format:
```
$N$ $X$
$P_2$ $P_3$ $\dots$ $P_N$
$B_1$ $W_1$ $C_1$
$B_2$ $W_2$ $C_2$
$\vdots$
$B_N$ $W_N$ $C_N$
```
```
$N$ $X$
$P_2$ $P_3$ $\dots$ $P_N$
$B_1$ $W_1$ $C_1$
$B_2$ $W_2$ $C_2$
$\vdots$
$B_N$ $W_N$ $C_N$
```
Output
Print $N$ lines. The $i$-th line should contain $F(i)$.
Constraints
- $2 \leq N \leq 200$
- $0 \leq X \leq 50000$
- $1 \leq P_i \leq i - 1$
- $0 \leq B_i \leq 10^{15}$
- $0 \leq W_i \leq X$
- $C_i$ is $0$ or $1$.
- All input values are integers.
- $0 \leq X \leq 50000$
- $1 \leq P_i \leq i - 1$
- $0 \leq B_i \leq 10^{15}$
- $0 \leq W_i \leq X$
- $C_i$ is $0$ or $1$.
- All input values are integers.
Sample 1 Input
4 10
1 2 2
2 1 0
4 2 1
6 8 0
7 4 1
Sample 1 Output
9
10
6
7
For v=1, choosing c=2 and then c=3 changes U as shown in the figure, making it a good rooted tree. The total beauty of the vertices in this tree is 2+7=9, which is the maximum among all good rooted trees, so F(1)=9.
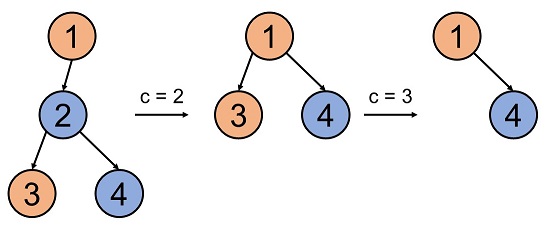
For v=2, choosing c=4 changes U as shown in the figure, making it a good rooted tree. The total beauty of the vertices in this tree is 4+6=10, which is the maximum among all good rooted trees, so F(2)=10.
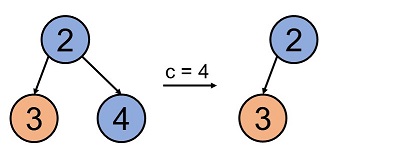

For v=2, choosing c=4 changes U as shown in the figure, making it a good rooted tree. The total beauty of the vertices in this tree is 4+6=10, which is the maximum among all good rooted trees, so F(2)=10.

Sample 2 Input
5 5
1 2 2 3
1 1 0
10 1 1
100 1 0
1000 1 1
10000 1 1
Sample 2 Output
11001
10110
10100
1000
10000
Sample 3 Input
20 100
1 2 1 1 1 6 6 5 1 7 9 4 6 4 15 16 8 2 5
887945036308847 12 0
699398807312293 20 1
501806283312516 17 0
559755618233839 19 1
253673279319163 10 1
745815685342299 11 1
251710263962529 15 0
777195295276573 15 0
408579800634972 17 0
521840965162492 17 1
730678137312837 18 1
370007714721362 14 1
474595536466754 17 0
879365432938644 15 0
291785577961862 20 0
835878893889428 14 1
503562238579284 10 0
567569163005307 18 1
368949585722534 15 0
386435396601075 16 0
Sample 3 Output
5329161389647368
1570154676347343
501806283312516
2665577865131167
1418696191276572
3952333977838189
982388401275366
1344764458281880
778587515356334
521840965162492
730678137312837
370007714721362
474595536466754
879365432938644
1631226710430574
1339441132468712
503562238579284
567569163005307
368949585722534
386435396601075