9931: ABC311 —— C - Find it!
[Creator : ]
Description
There is a directed graph with $N$ vertices and $N$ edges.
The $i$-th edge goes from vertex $i$ to vertex $A_i$. (The constraints guarantee that $i \neq A_i$.)
Find a directed cycle without the same vertex appearing multiple times.
It can be shown that a solution exists under the constraints of this problem.
Notes
The sequence of vertices $B = (B_1, B_2, \dots, B_M)$ is called a directed cycle when all of the following conditions are satisfied:
- $M \geq 2$
- The edge from vertex $B_i$ to vertex $B_{i+1}$ exists. $(1 \leq i \leq M-1)$
- The edge from vertex $B_M$ to vertex $B_1$ exists.
- If $i \neq j$, then $B_i \neq B_j$.
The $i$-th edge goes from vertex $i$ to vertex $A_i$. (The constraints guarantee that $i \neq A_i$.)
Find a directed cycle without the same vertex appearing multiple times.
It can be shown that a solution exists under the constraints of this problem.
Notes
The sequence of vertices $B = (B_1, B_2, \dots, B_M)$ is called a directed cycle when all of the following conditions are satisfied:
- $M \geq 2$
- The edge from vertex $B_i$ to vertex $B_{i+1}$ exists. $(1 \leq i \leq M-1)$
- The edge from vertex $B_M$ to vertex $B_1$ exists.
- If $i \neq j$, then $B_i \neq B_j$.
Input
The input is given from Standard Input in the following format:
```
$N$
$A_1$ $A_2$ $\dots$ $A_N$
```
```
$N$
$A_1$ $A_2$ $\dots$ $A_N$
```
Output
Print a solution in the following format:
```
$M$
$B_1$ $B_2$ $\dots$ $B_M$
```
$M$ is the number of vertices, and $B_i$ is the $i$-th vertex in the directed cycle.
The following conditions must be satisfied:
- $2 \le M$
- $B_{i+1} = A_{B_i}$ ( $1 \le i \le M-1$ )
- $B_{1} = A_{B_M}$
- $B_i \neq B_j$ ( $i \neq j$ )
If multiple solutions exist, any of them will be accepted.
```
$M$
$B_1$ $B_2$ $\dots$ $B_M$
```
$M$ is the number of vertices, and $B_i$ is the $i$-th vertex in the directed cycle.
The following conditions must be satisfied:
- $2 \le M$
- $B_{i+1} = A_{B_i}$ ( $1 \le i \le M-1$ )
- $B_{1} = A_{B_M}$
- $B_i \neq B_j$ ( $i \neq j$ )
If multiple solutions exist, any of them will be accepted.
Constraints
- All input values are integers.
- $2 \le N \le 2 \times 10^5$
- $1 \le A_i \le N$
- $A_i \neq i$
- $2 \le N \le 2 \times 10^5$
- $1 \le A_i \le N$
- $A_i \neq i$
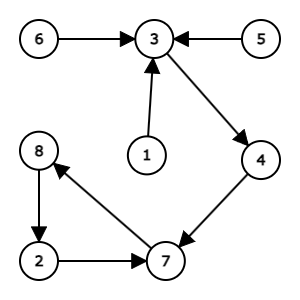
Sample 1 Input
7
6 7 2 1 3 4 5
Sample 1 Output
4
7 5 3 2
7→5→3→2→7 is indeed a directed cycle.
Here is the graph corresponding to this input:
Here are other acceptable outputs:
4 2 7 5 3
3 4 1 6
Note that the graph may not be connected.
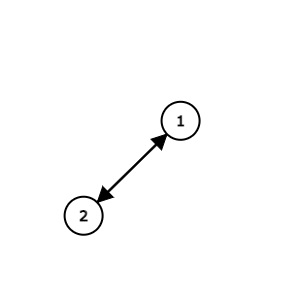
Sample 2 Input
2
2 1
Sample 2 Output
2
1 2
This case contains both of the edges 1→2 and 2→1.
In this case, 1→2→1 is indeed a directed cycle.
Here is the graph corresponding to this input, where 1↔2 represents the existence of both 1→2 and 2→1:
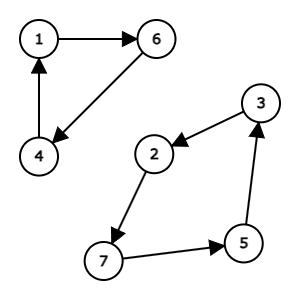
Sample 3 Input
8
3 7 4 7 3 3 8 2
Sample 3 Output
3
2 7 8
Here is the graph corresponding to this input: