9917: ABC310 —— G - Takahashi And Pass-The-Ball Game
[Creator : ]
Description
There are $N$ Takahashi.
The $i$-th Takahashi has an integer $A_i$ and $B_i$ balls.
An integer $x$ between $1$ and $K$, inclusive, will be chosen uniformly at random, and they will repeat the following operation $x$ times.
- For every $i$, the $i$-th Takahashi gives all his balls to the $A_i$-th Takahashi.
Beware that all $N$ Takahashi simultaneously perform this operation.
For each $i=1,2,\ldots,N$, find the expected value, modulo $998244353$, of the number of balls the $i$-th Takahashi has at the end of the operations.
How to find a expected value modulo $998244353$ It can be proved that the sought probability is always a rational number. Additionally, the constraints of this problem guarantee that if the sought probability is represented as an irreducible fraction $\frac{y}{x}$, then $x$ is not divisible by $998244353$. Here, there is a unique $0\leq z\lt998244353$ such that $y\equiv xz\pmod{998244353}$, so report this $z$.
The $i$-th Takahashi has an integer $A_i$ and $B_i$ balls.
An integer $x$ between $1$ and $K$, inclusive, will be chosen uniformly at random, and they will repeat the following operation $x$ times.
- For every $i$, the $i$-th Takahashi gives all his balls to the $A_i$-th Takahashi.
Beware that all $N$ Takahashi simultaneously perform this operation.
For each $i=1,2,\ldots,N$, find the expected value, modulo $998244353$, of the number of balls the $i$-th Takahashi has at the end of the operations.
How to find a expected value modulo $998244353$ It can be proved that the sought probability is always a rational number. Additionally, the constraints of this problem guarantee that if the sought probability is represented as an irreducible fraction $\frac{y}{x}$, then $x$ is not divisible by $998244353$. Here, there is a unique $0\leq z\lt998244353$ such that $y\equiv xz\pmod{998244353}$, so report this $z$.
Input
The input is given from Standard Input in the following format:
```
$N$ $K$
$A _ 1$ $A _ 2$ $\cdots$ $A _ N$
$B _ 1$ $B _ 2$ $\cdots$ $B _ N$
```
```
$N$ $K$
$A _ 1$ $A _ 2$ $\cdots$ $A _ N$
$B _ 1$ $B _ 2$ $\cdots$ $B _ N$
```
Output
Print the expected value of the number of balls the $i$-th Takahashi has at the end of the operations for $i=1,2,\ldots,N$, separated by spaces, in a single line.
Constraints
- $1\leq N\leq 2\times10^5$
- $1\leq K\leq 10^{18}$
- $K$ is not a multiple of $998244353$.
- $1\leq A _ i\leq N\ (1\leq i\leq N)$
- $0\leq B _ i\lt998244353\ (1\leq i\leq N)$
- All input values are integers.
- $1\leq K\leq 10^{18}$
- $K$ is not a multiple of $998244353$.
- $1\leq A _ i\leq N\ (1\leq i\leq N)$
- $0\leq B _ i\lt998244353\ (1\leq i\leq N)$
- All input values are integers.
Sample 1 Input
5 2
3 1 4 1 5
1 1 2 3 5
Sample 1 Output
3 0 499122179 499122178 5
During two operations, the five Takahashi have the following number of balls.
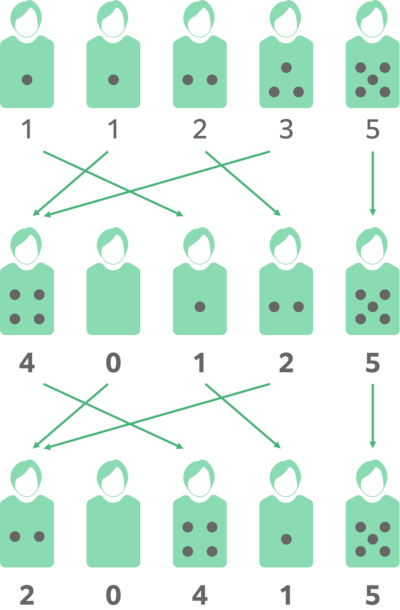
If x=1 is chosen, the five Takahashi have 4,0,1,2,5 balls.
If x=2 is chosen, the five Takahashi have 2,0,4,1,5 balls.
Thus, the sought expected values are $3,0,\frac{5}{2},\frac{3}{2},5$. Print these values modulo 998244353, that is, 3,0,499122179,499122178,5, separated by spaces.

If x=1 is chosen, the five Takahashi have 4,0,1,2,5 balls.
If x=2 is chosen, the five Takahashi have 2,0,4,1,5 balls.
Thus, the sought expected values are $3,0,\frac{5}{2},\frac{3}{2},5$. Print these values modulo 998244353, that is, 3,0,499122179,499122178,5, separated by spaces.
Sample 2 Input
3 1000
1 1 1
1 10 100
Sample 2 Output
111 0 0
After one or more operations, the first Takahashi gets all balls.
Sample 3 Input
16 1000007
16 12 6 12 1 8 14 14 5 7 6 5 9 6 10 9
719092922 77021920 539975779 254719514 967592487 476893866 368936979 465399362 342544824 540338192 42663741 165480608 616996494 16552706 590788849 221462860
Sample 3 Output
817852305 0 0 0 711863206 253280203 896552049 935714838 409506220 592088114 0 413190742 0 363914270 0 14254803
24 100000000007
19 10 19 15 1 20 13 15 8 23 22 16 19 22 2 20 12 19 17 20 16 8 23 6
944071276 364842194 5376942 671161415 477159272 339665353 176192797 2729865 676292280 249875565 259803120 103398285 466932147 775082441 720192643 535473742 263795756 898670859 476980306 12045411 620291602 593937486 761132791 746546443
918566373 436241503 0 0 0 455245534 0 356196743 0 906000633 0 268983266 21918337 0 733763572 173816039 754920403 0 273067118 205350062 0 566217111 80141532 0