9874: ABC305 —— F - Dungeon Explore
[Creator : ]
Description
This is an interactive problem (where your program and the judge program interact through Standard Input and Output).
There is a simple connected undirected graph with $N$ vertices and $M$ edges. The vertices are numbered with integers from $1$ to $N$.
Initially, you are at vertex $1$. Repeat moving to an adjacent vertex at most $2N$ times to reach vertex $N$.
Here, you do not initially know all edges of the graph, but you will be informed of the vertices adjacent to the vertex you are at.
There is a simple connected undirected graph with $N$ vertices and $M$ edges. The vertices are numbered with integers from $1$ to $N$.
Initially, you are at vertex $1$. Repeat moving to an adjacent vertex at most $2N$ times to reach vertex $N$.
Here, you do not initially know all edges of the graph, but you will be informed of the vertices adjacent to the vertex you are at.
Input
First, receive the number of vertices $N$ and the number of edges $M$ in the graph from Standard Input:
```
$N$ $M$
```
Next, you get to repeat the operation described in the problem statement at most $2N$ times against the judge.
At the beginning of each operation, the vertices adjacent to the vertex you are currently at are given from Standard Input in the following format:
```
$k$ $v _ 1$ $v _ 2$ $\ldots$ $v _ k$
```
Here, $v _ i\ (1\leq i\leq k)$ are integers between $1$ and $N$ such that $v _ 1\lt v _ 2\lt\cdots\lt v _ k$.
Choose one of $v _ i\ (1\leq i\leq k)$ and print it to Standard Output in the following format:
```
$v _ i$
```
After this operation, you will be at vertex $v _ i$.
If you perform more than $2N$ operations or print invalid output, the judge will send `-1` to Standard Input.
If the destination of a move is vertex $N$, the judge will send `OK` to Standard Input and terminate.
```
$N$ $M$
```
Next, you get to repeat the operation described in the problem statement at most $2N$ times against the judge.
At the beginning of each operation, the vertices adjacent to the vertex you are currently at are given from Standard Input in the following format:
```
$k$ $v _ 1$ $v _ 2$ $\ldots$ $v _ k$
```
Here, $v _ i\ (1\leq i\leq k)$ are integers between $1$ and $N$ such that $v _ 1\lt v _ 2\lt\cdots\lt v _ k$.
Choose one of $v _ i\ (1\leq i\leq k)$ and print it to Standard Output in the following format:
```
$v _ i$
```
After this operation, you will be at vertex $v _ i$.
If you perform more than $2N$ operations or print invalid output, the judge will send `-1` to Standard Input.
If the destination of a move is vertex $N$, the judge will send `OK` to Standard Input and terminate.
When receiving `-1` or `OK`, immediately terminate the program.
Notes
- In each output, insert a newline at the end and flush Standard Output. Otherwise, the verdict may be TLE.
- The verdict will be indeterminate if the program prints invalid output or quits prematurely in the middle of the interaction.
- Terminate the program immediately after reaching vertex $N$. Otherwise, the verdict will be indeterminate.
- The judge for this problem is adaptive. This means that the graph may change without contradicting the constraints or previous outputs.
Output
In the following sample interaction, we have $N=4$, $M=5$, and the graph in the figure below.
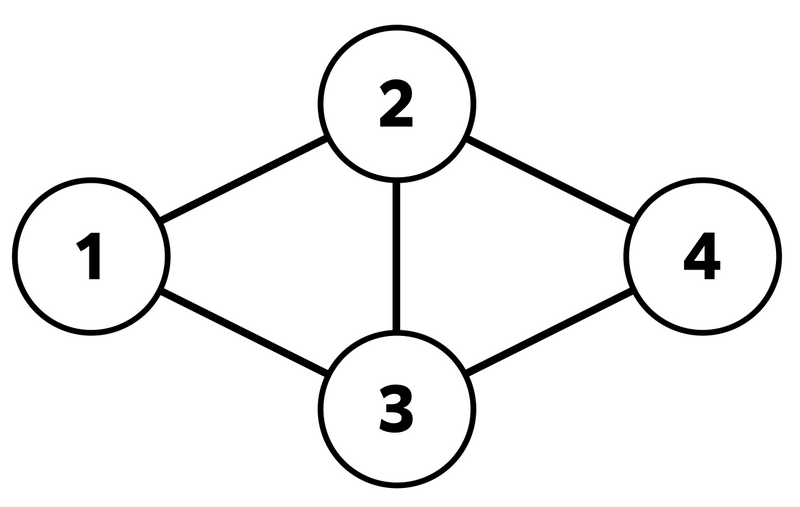

Constraints
- $2\leq N\leq100$
- $N-1\leq M\leq\dfrac{N(N-1)}2$
- The graph is simple and connected.
- All input values are integers.
- $N-1\leq M\leq\dfrac{N(N-1)}2$
- The graph is simple and connected.
- All input values are integers.