【基础概念】

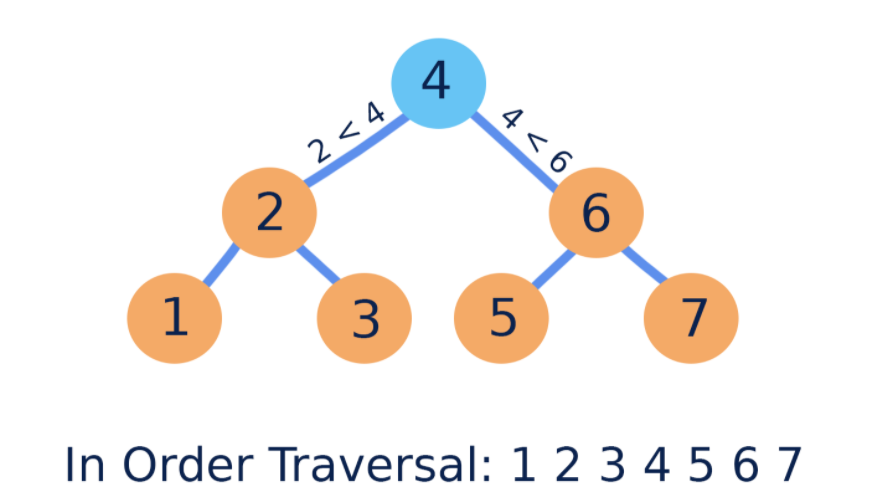
BST树，英文全称:Binary Search Tree，被称为二叉查找树或二叉搜索树。
如果一个二叉查找树非空，那么它具有如下性质：
1. 左子树上所有节点的值小于根节点的值，节点上的值沿着边的方向递减。
2. 右子树上所有节点的值大于根节点的值，节点上的值沿着边的方向递增。
3. 非空的左子树和右子树也分别是二叉查找树。
4. 按照中序遍历(左子树->根节点->右子树)的方式遍历该二叉查找树，可以得到一个递增的有序序列。

【基本操作】

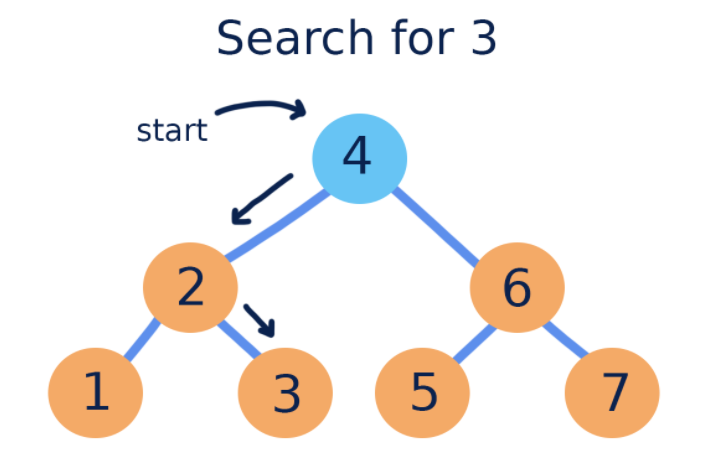
【查找节点】

1.从树的根节点开始移动。
2.如果被查找值小于当前节点，则向左移动。
3.如果被查找值大于当前节点，则向右移动。

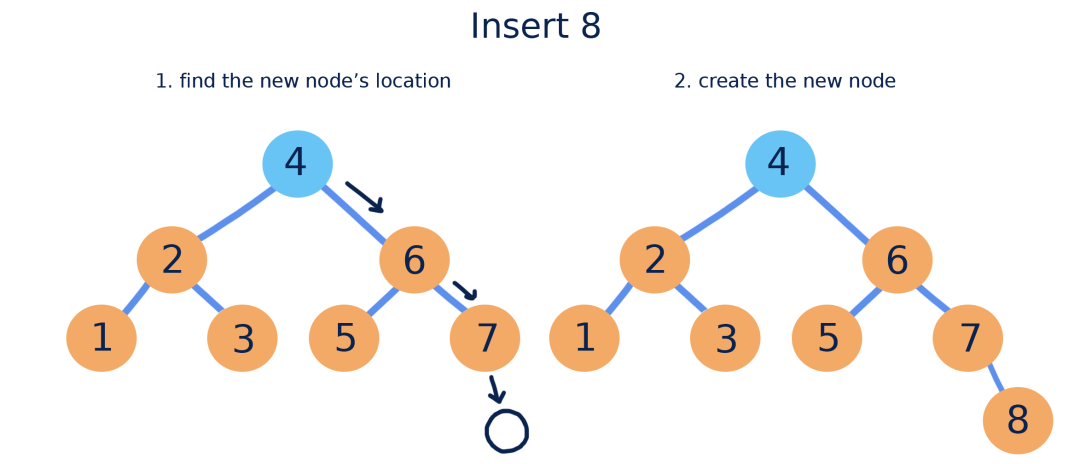
【插入节点】

1.先执行查找操作，来确定新节点的位置。
2.确认位置后，插入新节点，新节点成为叶子节点。

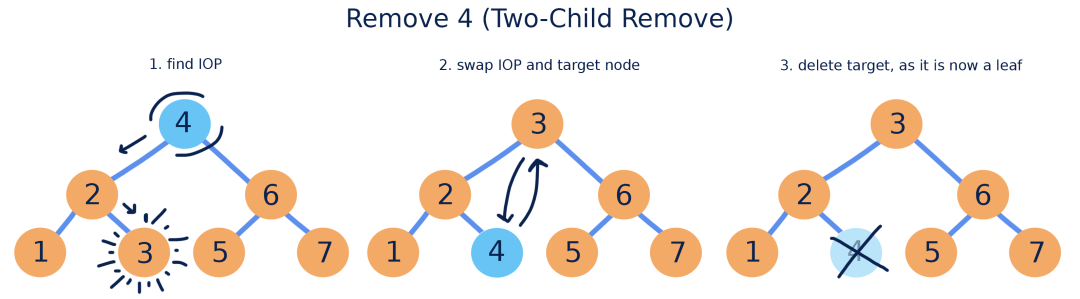
【删除节点】

从BST树删除节点时，我们关心的是保持树的其余节点以正确的顺序排列。
删除节点的实际操作是将节点替换为NULL。
根据删除节点的位置不同，分下面三种情况：
(1) 要删除的节点是叶子节点。简单执行删除操作。

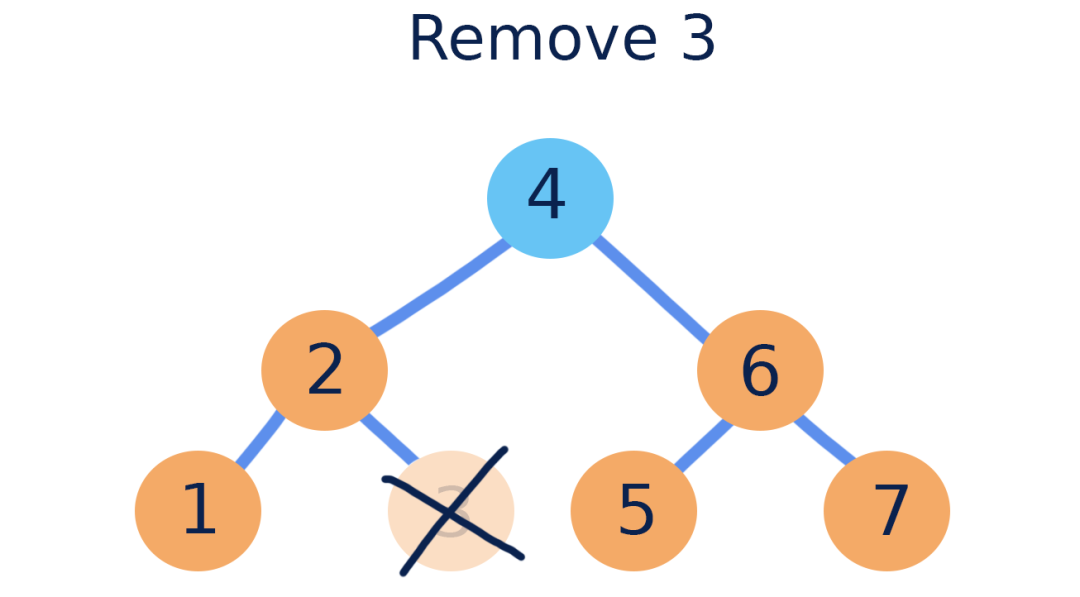
(2) 如果节点只有一个子节点。删除后，用子节点填充它原来的位置。

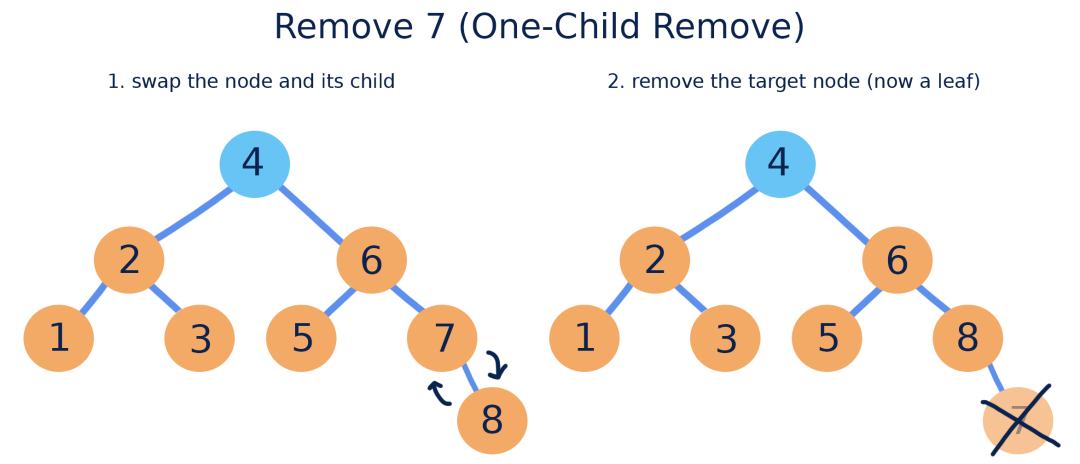
(3) 如果节点有两个子节点。根据大小，将它和左子树的最大节点交换，或者和右子树的最小节点交换。因为左子树的最大节点是叶子节点，没有右子节点且不会继续扩展，右子树的最小节点也是叶子节点，没有左子节点且不会继续扩展。