二叉搜索树 (BST) 递归定义为具有以下属性的二叉树：

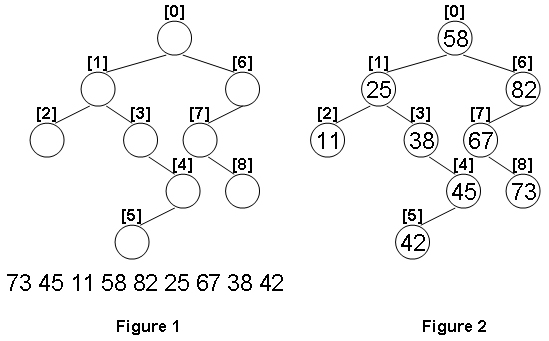
• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值
• 若它的右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值
• 它的左、右子树也分别为二叉搜索树

二叉搜索树有一个特殊的性质：二叉搜索树的中序遍历是一个有序序列。
给定二叉树的具体结构以及一系列不同的整数，只有一种方法可以将这些数填充到树中，以使结果树满足 BST 的定义。
请你输出结果树的层序遍历。
示例如图 1 和图 2 所示。

第一行包含一个正整数 $N\ (1 \leq N \leq 2\times 10^5)$，表示树的结点个数。所有结点的编号为 $0\sim N-1$，并且编号为 $0$ 的结点是根结点。
接下来 $N$ 行，第 $i$ 行（从 $0$ 计数）包含结点 $i$ 的左右子结点编号。如果该结点的某个子结点不存在，则用 $-1$ 表示。
最后一行，包含 $N$ 个不同的整数，表示要插入树中的数值。

输出结果树的层序遍历。