9841: ABC302 —— B - Find snuke
[Creator : ]
Description
There is a grid with $H$ horizontal rows and $W$ vertical columns. Each cell has a lowercase English letter written on it. We denote by $(i, j)$ the cell at the $i$-th row from the top and $j$-th column from the left.
The letters written on the grid are represented by $H$ strings $S_1,S_2,\ldots, S_H$, each of length $W$. The $j$-th letter of $S_i$ represents the letter written on $(i, j)$.
There is a unique set of contiguous cells (going vertically, horizontally, or diagonally) in the grid with `s`, `n`, `u`, `k`, and `e` written on them in this order.
Find the positions of such cells and print them in the format specified in the Output section.
A tuple of five cells $(A_1,A_2,A_3,A_4,A_5)$ is said to form a set of contiguous cells (going vertically, horizontally, or diagonally) with `s`, `n`, `u`, `k`, and `e` written on them in this order if and only if all of the following conditions are satisfied.
- $A_1,A_2,A_3,A_4$ and $A_5$ have letters `s`, `n`, `u`, `k`, and `e` written on them, respectively.
- For all $1\leq i\leq 4$, cells $A_i$ and $A_{i+1}$ share a corner or a side.
- The centers of $A_1,A_2,A_3,A_4$, and $A_5$ are on a common line at regular intervals.
The letters written on the grid are represented by $H$ strings $S_1,S_2,\ldots, S_H$, each of length $W$. The $j$-th letter of $S_i$ represents the letter written on $(i, j)$.
There is a unique set of contiguous cells (going vertically, horizontally, or diagonally) in the grid with `s`, `n`, `u`, `k`, and `e` written on them in this order.
Find the positions of such cells and print them in the format specified in the Output section.
A tuple of five cells $(A_1,A_2,A_3,A_4,A_5)$ is said to form a set of contiguous cells (going vertically, horizontally, or diagonally) with `s`, `n`, `u`, `k`, and `e` written on them in this order if and only if all of the following conditions are satisfied.
- $A_1,A_2,A_3,A_4$ and $A_5$ have letters `s`, `n`, `u`, `k`, and `e` written on them, respectively.
- For all $1\leq i\leq 4$, cells $A_i$ and $A_{i+1}$ share a corner or a side.
- The centers of $A_1,A_2,A_3,A_4$, and $A_5$ are on a common line at regular intervals.
Input
The input is given from Standard Input in the following format:
```
$H$ $W$
$S_1$
$S_2$
$\vdots$
$S_H$
```
```
$H$ $W$
$S_1$
$S_2$
$\vdots$
$S_H$
```
Output
Print five lines in the following format.
Let $(R_1,C_1), (R_2,C_2)\ldots,(R_5,C_5)$ be the cells in the sought set with `s`, `n`, `u`, `k`, and `e` written on them, respectively. The $i$-th line should contain $R_i$ and $C_i$ in this order, separated by a space.
In other words, print them in the following format:
```
$R_1$ $C_1$
$R_2$ $C_2$
$\vdots$
$R_5$ $C_5$
```
See also Sample Inputs and Outputs below.
Let $(R_1,C_1), (R_2,C_2)\ldots,(R_5,C_5)$ be the cells in the sought set with `s`, `n`, `u`, `k`, and `e` written on them, respectively. The $i$-th line should contain $R_i$ and $C_i$ in this order, separated by a space.
In other words, print them in the following format:
```
$R_1$ $C_1$
$R_2$ $C_2$
$\vdots$
$R_5$ $C_5$
```
See also Sample Inputs and Outputs below.
Constraints
- $5\leq H\leq 100$
- $5\leq W\leq 100$
- $H$ and $W$ are integers.
- $S_i$ is a string of length $W$ consisting of lowercase English letters.
- The given grid has a unique conforming set of cells.
- $5\leq W\leq 100$
- $H$ and $W$ are integers.
- $S_i$ is a string of length $W$ consisting of lowercase English letters.
- The given grid has a unique conforming set of cells.
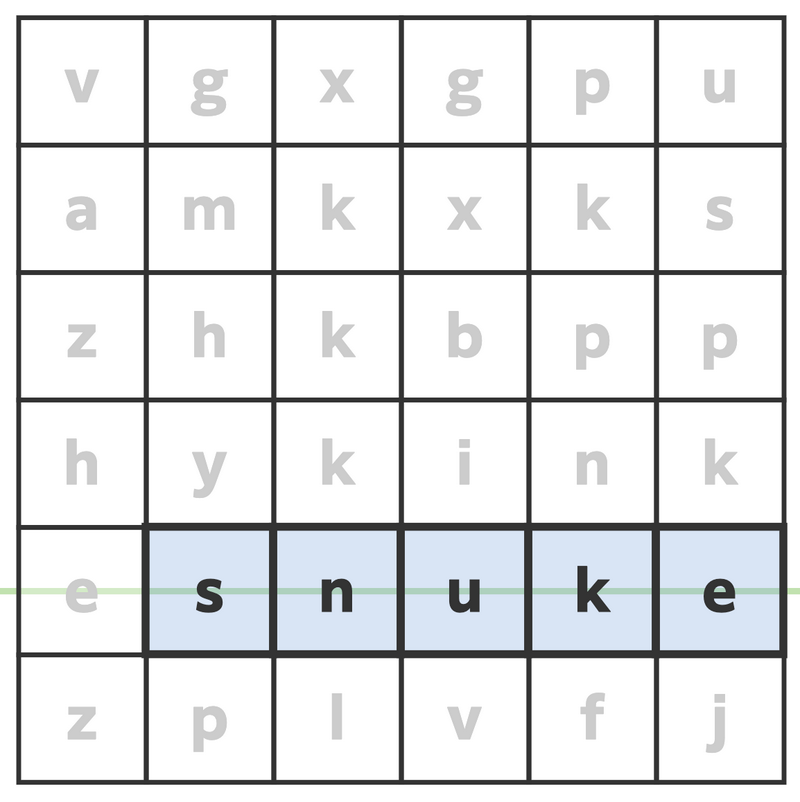
Sample 1 Input
6 6
vgxgpu
amkxks
zhkbpp
hykink
esnuke
zplvfj
Sample 1 Output
5 2
5 3
5 4
5 5
5 6
Tuple $(A_1,A_2,A_3,A_4,A_5)=((5,2),(5,3),(5,4),(5,5),(5,6))$ satisfies the conditions.
Indeed, the letters written on them are s, n, u, k, and e;
for all $1≤i≤4$, cells $A_i$ and $A_{i+1}$ share a side;
Indeed, the letters written on them are s, n, u, k, and e;
for all $1≤i≤4$, cells $A_i$ and $A_{i+1}$ share a side;
and the centers of the cells are on a common line.
Sample 2 Input
5 5
ezzzz
zkzzz
ezuzs
zzznz
zzzzs
Sample 2 Output
5 5
4 4
3 3
2 2
1 1
Tuple $(A_1,A_2,A_3,A_4,A_5)=((5,5),(4,4),(3,3),(2,2),(1,1))$ satisfies the conditions.
However, for example, $(A_1,A_2,A_3,A_4,A_5)=((3,5),(4,4),(3,3),(2,2),(3,1))$ violates the third condition because the centers of the cells are not on a common line, although it satisfies the first and second conditions.
However, for example, $(A_1,A_2,A_3,A_4,A_5)=((3,5),(4,4),(3,3),(2,2),(3,1))$ violates the third condition because the centers of the cells are not on a common line, although it satisfies the first and second conditions.
Sample 3 Input
10 10
kseeusenuk
usesenesnn
kskekeeses
nesnusnkkn
snenuuenke
kukknkeuss
neunnennue
sknuessuku
nksneekknk
neeeuknenk
Sample 3 Output
9 3
8 3
7 3
6 3
5 3