We have a connected undirected graph with $N$ vertices numbered $1$ to $N$ and $M$ edges numbered $1$ to $M$. Edge $i$ connects vertex $U_i$ and vertex $V_i$, and has an integer weight of $W_i$. For $1\leq s,t \leq N,\ s\neq t$, let us define $d(s,t)$ as follows.

-   For every path connecting vertex $s$ and vertex $t$, consider the maximum weight of an edge along that path. $d(s,t)$ is the minimum value of this weight.

Answer $Q$ queries. The $j$-th query is as follows.

-   You are given $A_j,S_j,T_j$. By what value will $d(S_j,T_j)$ increase when the weight of edge $A_j$ is increased by $1$?

Note that each query does not actually change the weight of the edge.

The input is given from Standard Input in the following format:

```
$N$ $M$
$U_1$ $V_1$ $W_1$
$\vdots$
$U_M$ $V_M$ $W_M$
$Q$
$A_1$ $S_1$ $T_1$
$\vdots$
$A_Q$ $S_Q$ $T_Q$
```

Print $Q$ lines. The $j$-th line $(1\leq j \leq Q)$ should contain the answer to the $j$-th query.

-   $2\leq N \leq 2\times 10^5$
-   $N-1\leq M \leq 2\times 10^5$
-   $1 \leq U_i,V_i \leq N$
-   $U_i \neq V_i$
-   $1 \leq W_i \leq M$
-   The given graph is connected.
-   $1\leq Q \leq 2\times 10^5$
-   $1 \leq A_j \leq M$
-   $1 \leq S_j,T_j \leq N$
-   $S_j\neq T_j$
-   All values in the input are integers.

0
0
0
0
0
1
1

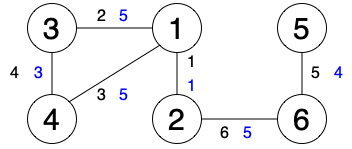
The above figure shows the edge numbers in black and the edge weights in blue.
Let us explain the first through sixth queries.
First, consider d(4,6) in the given graph. The maximum weight of an edge along the path 4→1→2→6 is 5, which is the minimum over all paths connecting vertex 4 and vertex 6, so d(4,6)=5.
Next, consider the increment of d(4,6) when the weight of edge x (1≤x≤6) increases by 1. When x=6, we have d(4,6)=6, and the increment is 1. On the other hand, when x≠6, we have d(4,6)=5, and the increment is 0. For instance, when x=3, the maximum weight of an edge along the path 4→1→2→6 is 6, but the maximum weight of an edge along the path 4→3→1→2→6 is 5, so d(4,6) is still 5.

0

The given graph may contain multi-edges.