9817: ABC300 —— C - Cross
[Creator : ]
Description
We have a grid with $H$ horizontal rows and $W$ vertical columns. We denote by $(i, j)$ the cell at the $i$-th row from the top and $j$-th column from the left of the grid.
Each cell in the grid has a symbol `$\#$` or `.` written on it. Let $C[i][j]$ be the character written on $(i, j)$. For integers $i$ and $j$ such that at least one of $1 \leq i \leq H$ and $1 \leq j \leq W$ is violated, we define $C[i][j]$ to be `.`.
$(4n+1)$ squares, consisting of $(a, b)$ and $(a+d,b+d),(a+d,b-d),(a-d,b+d),(a-d,b-d)$ $(1 \leq d \leq n, 1 \leq n)$, are said to be a cross of size $n$ centered at $(a,b)$ if and only if all of the following conditions are satisfied:
- C[a] is $\#$.
- $C[a+d][b+d],C[a+d][b-d],C[a-d][b+d]$, and $C[a-d][b-d]$ are all $\#$, for all integers $d$ such that $1 \leq d \leq n$,
- At least one of $C[a+n+1][b+n+1],C[a+n+1][b-n-1],C[a-n-1][b+n+1]$, and $C[a-n-1][b-n-1]$ is `.`.
For example, the grid in the following figure has a cross of size $1$ centered at $(2, 2)$ and another of size $2$ centered at $(3, 7)$.
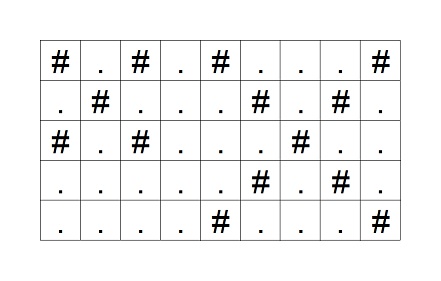
The grid has some crosses. No `$\#$` is written on the cells except for those comprising a cross.
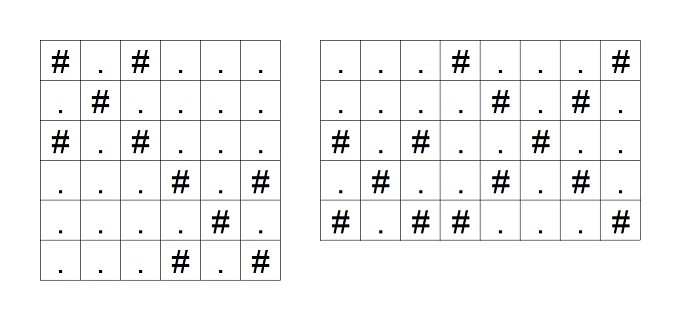
Additionally, no two squares that comprise two different crosses share a corner. The two grids in the following figure are the examples of grids where two squares that comprise different crosses share a corner; such grids are not given as an input. For example, the left grid is invalid because $(3, 3)$ and $(4, 4)$ share a corner.
Let $N = \min(H, W)$, and $S_n$ be the number of crosses of size $n$. Find $S_1, S_2, \dots, S_N$.
Each cell in the grid has a symbol `$\#$` or `.` written on it. Let $C[i][j]$ be the character written on $(i, j)$. For integers $i$ and $j$ such that at least one of $1 \leq i \leq H$ and $1 \leq j \leq W$ is violated, we define $C[i][j]$ to be `.`.
$(4n+1)$ squares, consisting of $(a, b)$ and $(a+d,b+d),(a+d,b-d),(a-d,b+d),(a-d,b-d)$ $(1 \leq d \leq n, 1 \leq n)$, are said to be a cross of size $n$ centered at $(a,b)$ if and only if all of the following conditions are satisfied:
- C[a] is $\#$.
- $C[a+d][b+d],C[a+d][b-d],C[a-d][b+d]$, and $C[a-d][b-d]$ are all $\#$, for all integers $d$ such that $1 \leq d \leq n$,
- At least one of $C[a+n+1][b+n+1],C[a+n+1][b-n-1],C[a-n-1][b+n+1]$, and $C[a-n-1][b-n-1]$ is `.`.
For example, the grid in the following figure has a cross of size $1$ centered at $(2, 2)$ and another of size $2$ centered at $(3, 7)$.

The grid has some crosses. No `$\#$` is written on the cells except for those comprising a cross.
Additionally, no two squares that comprise two different crosses share a corner. The two grids in the following figure are the examples of grids where two squares that comprise different crosses share a corner; such grids are not given as an input. For example, the left grid is invalid because $(3, 3)$ and $(4, 4)$ share a corner.

Let $N = \min(H, W)$, and $S_n$ be the number of crosses of size $n$. Find $S_1, S_2, \dots, S_N$.
Input
The input is given from Standard Input in the following format:
```
$H$ $W$
$C[1][1]C[1][2]\dots C[1][W]$
$C[2][1]C[2][2]\dots C[2][W]$
$\vdots$
$C[H][1]C[H][2]\dots C[H][W]$
```
```
$H$ $W$
$C[1][1]C[1][2]\dots C[1][W]$
$C[2][1]C[2][2]\dots C[2][W]$
$\vdots$
$C[H][1]C[H][2]\dots C[H][W]$
```
Output
Print $S_1, S_2, \dots$, and $S_N$, separated by spaces.
Constraints
- $3 \leq H, W \leq 100$
- $C[i][j]$ is `#` or `.`.
- No two different squares that comprise two different crosses share a corner.
- $H$ and $W$ are integers.
- $C[i][j]$ is `#` or `.`.
- No two different squares that comprise two different crosses share a corner.
- $H$ and $W$ are integers.
Sample 1 Input
5 9
#.#.#...#
.#...#.#.
#.#...#..
.....#.#.
....#...#
Sample 1 Output
1 1 0 0 0
As described in the Problem Statement, there are a cross of size 1 centered at (2,2) and another of size 2 centered at (3,7).
Sample 2 Input
3 3
...
...
...
Sample 2 Output
0 0 0
There may be no cross.
Sample 3 Input
3 16
#.#.....#.#..#.#
.#.......#....#.
#.#.....#.#..#.#
Sample 3 Output
3 0 0
15 20
#.#..#.............#
.#....#....#.#....#.
#.#....#....#....#..
........#..#.#..#...
#.....#..#.....#....
.#...#....#...#..#.#
..#.#......#.#....#.
...#........#....#.#
..#.#......#.#......
.#...#....#...#.....
#.....#..#.....#....
........#.......#...
#.#....#....#.#..#..
.#....#......#....#.
#.#..#......#.#....#
5 0 1 0 0 0 1 0 0 0 0 0 0 0 0