9814: ABC265 —— Ex - No-capture Lance Game
[Creator : ]
Description
There is a grid with $H$ horizontal rows and $W$ vertical columns, and $(2 \times H)$ pieces. We consider the following game using them.
Two players take alternating turns. The game progresses as follows.
- In the initial state, every row contains one piece of the first player facing left and one piece of the second player facing right.
- The two players alternately advance one of their pieces.
- The player who is first to be unable to make a move loses, and the other player wins.
Let $(i, j)$ denote the square at the $i$-th row from the top and $j$-th column from the left. The following moves are allowed:
- The first player can move a piece at $(i,j)$ to $(i,k)$ if $k \lt j$ and none of $(i,k),(i,k+1),\dots,(i,j-1)$ contains a piece of either player.
- The second player can move a piece at $(i,j)$ to $(i,k)$ if $k \gt j$ and none of $(i,j+1),(i,j+2),\dots,(i,k)$ contains a piece of either player.
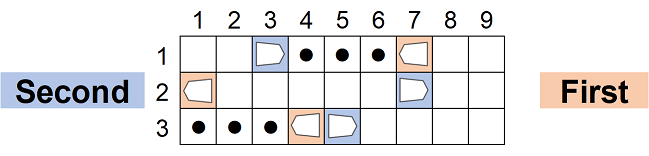
For example, in the figure below, on a $3\times 9$ grid, the first player's pieces are at $(1,7),(2,1),(3,4)$, and the second player's pieces are at $(1,3),(2,7),(3,5)$.
The first player can move the piece at $(1,7)$ to $(1,4),(1,5)$, or $(1,6)$, and the piece at $(3,4)$ to $(3,1),(3,2)$, or $(3,3)$. The first player cannot move the piece at $(2,1)$.
Currently, there is no piece on the grid. There are $\left\lbrace W(W-1)\right\rbrace^H$ ways to place one piece of the first player and one piece of the second player in each row, so that no two pieces are placed at the same square. How many of them satisfy the following condition? Find the count modulo $998244353$.
- When they play the game optimally from that initial state, the first player wins.
Two players take alternating turns. The game progresses as follows.
- In the initial state, every row contains one piece of the first player facing left and one piece of the second player facing right.
- The two players alternately advance one of their pieces.
- The player who is first to be unable to make a move loses, and the other player wins.
Let $(i, j)$ denote the square at the $i$-th row from the top and $j$-th column from the left. The following moves are allowed:
- The first player can move a piece at $(i,j)$ to $(i,k)$ if $k \lt j$ and none of $(i,k),(i,k+1),\dots,(i,j-1)$ contains a piece of either player.
- The second player can move a piece at $(i,j)$ to $(i,k)$ if $k \gt j$ and none of $(i,j+1),(i,j+2),\dots,(i,k)$ contains a piece of either player.
For example, in the figure below, on a $3\times 9$ grid, the first player's pieces are at $(1,7),(2,1),(3,4)$, and the second player's pieces are at $(1,3),(2,7),(3,5)$.
The first player can move the piece at $(1,7)$ to $(1,4),(1,5)$, or $(1,6)$, and the piece at $(3,4)$ to $(3,1),(3,2)$, or $(3,3)$. The first player cannot move the piece at $(2,1)$.

Currently, there is no piece on the grid. There are $\left\lbrace W(W-1)\right\rbrace^H$ ways to place one piece of the first player and one piece of the second player in each row, so that no two pieces are placed at the same square. How many of them satisfy the following condition? Find the count modulo $998244353$.
- When they play the game optimally from that initial state, the first player wins.
Input
Input is given from Standard Input in the following format:
```
$H$ $W$
```
```
$H$ $W$
```
Output
Print the answer.
Constraints
- $1 \leq H \leq 8000$
- $2 \leq W \leq 30$
- $H$ and $W$ are integers.
- $2 \leq W \leq 30$
- $H$ and $W$ are integers.
Sample 1 Input
1 3
Sample 1 Output
2
The first player can win if:
- the first player's piece is placed at (1,3), and the second player's piece is placed at (1,1); or
- the first player's piece is placed at (1,2), and the second player's piece is placed at (1,3).
Sample 2 Input
9 9
Sample 2 Output
583962987
Sample 3 Input
265 30
Sample 3 Output
366114675