There is an infinite two-dimensional grid, and we have a piece called Super Ryuma at square $(r_1, c_1)$.  (Ryu means dragon and Ma means horse.) In one move, the piece can go to one of the squares shown below:

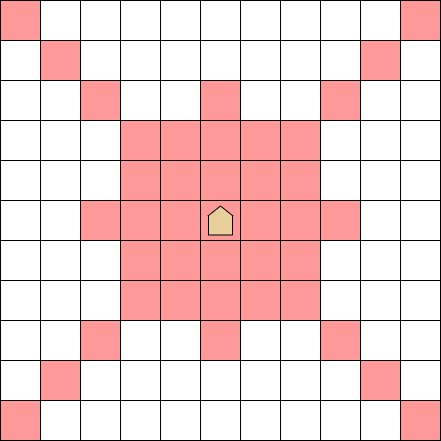
More formally, when Super Ryuma is at square $(a, b)$, it can go to square $(c, d)$ such that at least one of the following holds:

-   $a + b = c + d$
-   $a - b = c - d$
-   $|a - c| + |b - d| \le 3$

Find the minimum number of moves needed for the piece to reach $(r_2, c_2)$ from $(r_1, c_1)$.

Input is given from Standard Input in the following format:

```
$r_1$ $c_1$
$r_2$ $c_2$
```

Print the minimum number of moves needed for Super Ryuma to reach $(r_2, c_2)$ from $(r_1, c_1)$.

-   All values in input are integers.
-   $1 \le r_1, c_1, r_2, c_2 \le 10^9$

2

We need two moves - for example, (1,1)→(5,5)→(5,6).

2

We need two moves - for example, (1,1)→(100001,100001)→(1,200001).

3

We need three moves - for example, (2,3)→(3,3)→(−247,253)→(998244353,998244853).