Problem9652--ABC179 —— F - Simplified Reversi

9652: ABC179 —— F - Simplified Reversi

[Creator : ]
Time Limit : 1.000 sec  Memory Limit : 512 MiB

SubmitSolved: 1Submit Num: 1StatisticsShowOff!

Description

There is a grid with $N$ rows and $N$ columns of squares. Let $(i, j)$ be the square at the $i$-th row from the top and the $j$-th column from the left.

Each of the central $(N-2) \times (N-2)$ squares in the grid has a black stone on it. Each of the $2N - 1$ squares on the bottom side and the right side has a white stone on it.

$Q$ queries are given. We ask you to process them in order. There are two kinds of queries. Their input format and description are as follows:

-   `1 x`: Place a white stone on $(1, x)$. After that, for each black stone between $(1, x)$ and the first white stone you hit if you go down from $(1, x)$, replace it with a white stone.
-   `2 x`: Place a white stone on $(x, 1)$. After that, for each black stone between $(x, 1)$ and the first white stone you hit if you go right from $(x, 1)$, replace it with a white stone.

How many black stones are there on the grid after processing all $Q$ queries?

Input

Input is given from Standard Input in the following format:

```
$N$ $Q$
$Query_1$
$\vdots$
$Query_Q$
```

Output

Print how many black stones there are on the grid after processing all $Q$ queries.

Constraints

-   $3 \leq N \leq 2\times 10^5$
-   $0 \leq Q \leq \min(2N-4,2\times 10^5)$
-   $2 \leq x \leq N-1$
-   Queries are pairwise distinct.

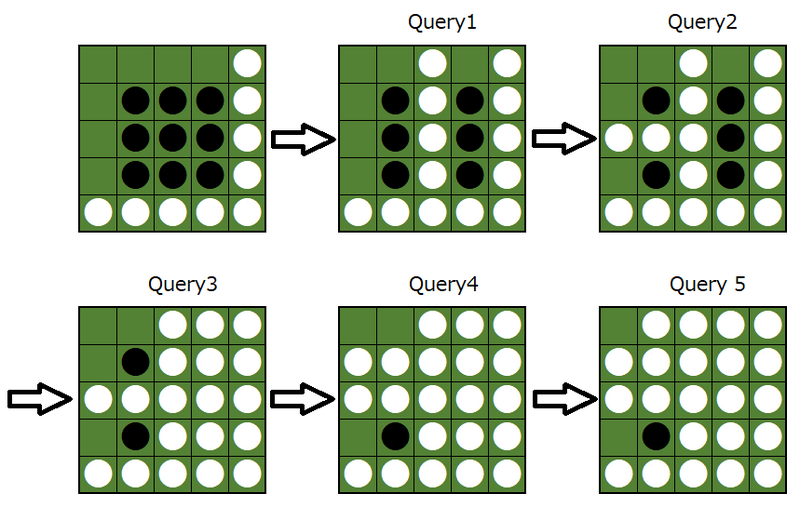
Sample 1 Input 

5 5
1 3
2 3
1 4
2 2
1 2

Sample 1 Output 

1

After each query, the grid changes in the following way:

Sample 2 Input 

200000 0

Sample 2 Output 

39999200004

Sample 3 Input 

176527 15
1 81279
2 22308
2 133061
1 80744
2 44603
1 170938
2 139754
2 15220
1 172794
1 159290
2 156968
1 56426
2 77429
1 97459
2 71282

Sample 3 Output 

31159505795

Source/Category

 
Submit