You are given $N$ circles on the $xy$-coordinate plane. For each $i = 1, 2, \ldots, N$, the $i$-th circle is centered at $(x_i, y_i)$ and has a radius of $r_i$.

Determine whether it is possible to get from $(s_x, s_y)$ to $(t_x, t_y)$ by only passing through points that lie on the circumference of at least one of the $N$ circles.

Input is given from Standard Input in the following format:

```
$N$
$s_x$ $s_y$ $t_x$ $t_y$
$x_1$ $y_1$ $r_1$
$x_2$ $y_2$ $r_2$
$\vdots$
$x_N$ $y_N$ $r_N$
```

If it is possible to get from $(s_x, s_y)$ to $(t_x, t_y)$, print `Yes`; otherwise, print `No`. Note that the judge is case-sensitive.

-   $1 \leq N \leq 3000$
-   $-10^9 \leq x_i, y_i \leq 10^9$
-   $1 \leq r_i \leq 10^9$
-   $(s_x, s_y)$ lies on the circumference of at least one of the $N$ circles.
-   $(t_x, t_y)$ lies on the circumference of at least one of the $N$ circles.
-   All values in input are integers.

Yes

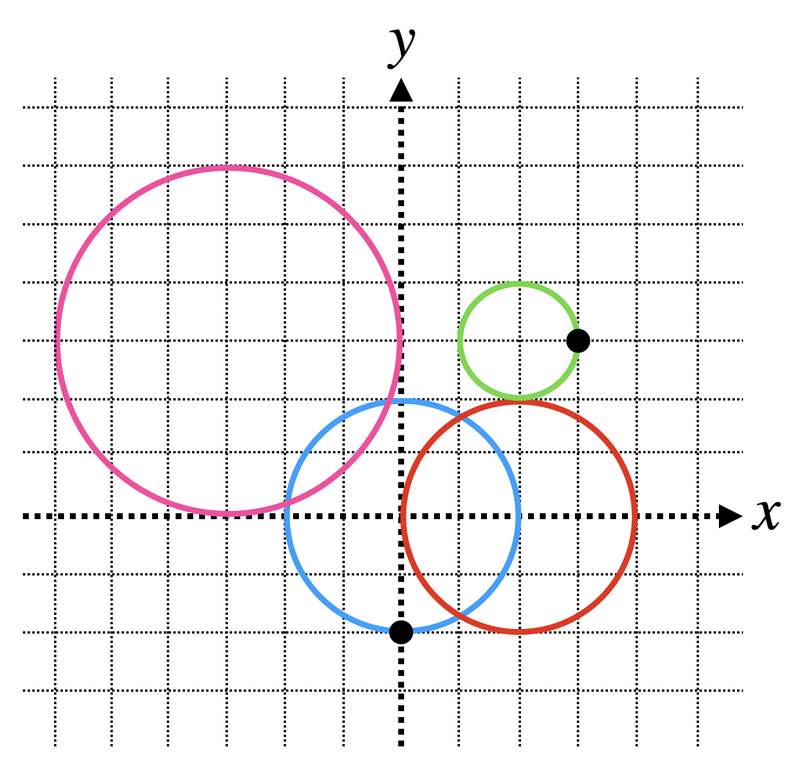
Here is one way to get from (0,−2) to (3,3).

• From (0,−2), pass through the circumference of the 1-st circle counterclockwise to reach (1,−3).
• From (1,−3), pass through the circumference of the 2-nd circle clockwise to reach (2,2).
• From (2,2), pass through the circumference of the 3-rd circle counterclockwise to reach (3,3).

Thus, Yes should be printed.

No

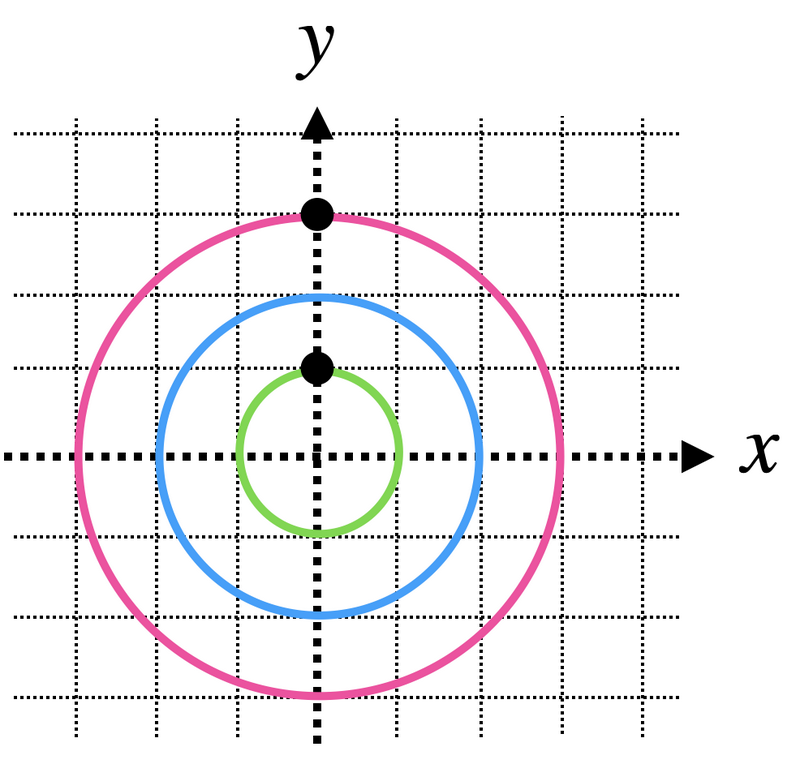
It is impossible to get from (0,1) to (0,3) by only passing through points on the circumference of at least one of the circles, so No should be printed.