9579: ABC243 —— C - Collision 2
[Creator : ]
Description
There are $N$ people in an $xy$-plane. Person $i$ is at $(X_i, Y_i)$. The positions of all people are different.
We have a string $S$ of length $N$ consisting of `L` and `R`.
If $S_i =$ `R`, Person $i$ is facing right; if $S_i =$ `L`, Person $i$ is facing left. All people simultaneously start walking in the direction they are facing. Here, right and left correspond to the positive and negative $x$-direction, respectively.
For example, the figure below shows the movement of people when $(X_1, Y_1) = (2, 3), (X_2, Y_2) = (1, 1), (X_3, Y_3) =(4, 1), S =$ `RRL`.
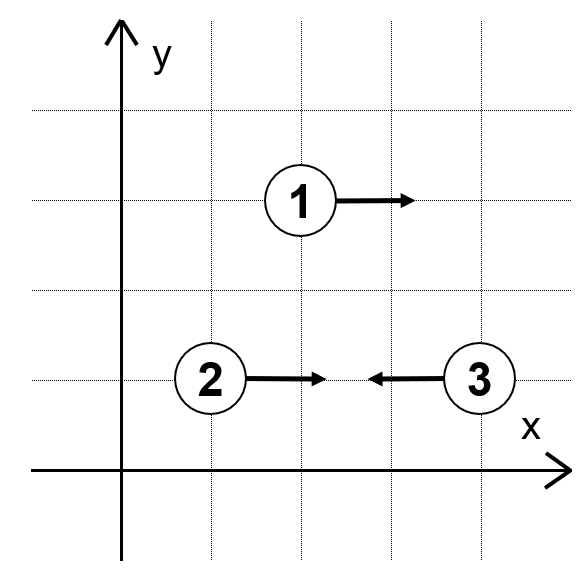
We say that there is a collision when two people walking in opposite directions come to the same position. Will there be a collision if all people continue walking indefinitely?
We have a string $S$ of length $N$ consisting of `L` and `R`.
If $S_i =$ `R`, Person $i$ is facing right; if $S_i =$ `L`, Person $i$ is facing left. All people simultaneously start walking in the direction they are facing. Here, right and left correspond to the positive and negative $x$-direction, respectively.
For example, the figure below shows the movement of people when $(X_1, Y_1) = (2, 3), (X_2, Y_2) = (1, 1), (X_3, Y_3) =(4, 1), S =$ `RRL`.

We say that there is a collision when two people walking in opposite directions come to the same position. Will there be a collision if all people continue walking indefinitely?
Input
Input is given from Standard Input in the following format:
```
$N$
$X_1$ $Y_1$
$X_2$ $Y_2$
$\vdots$
$X_N$ $Y_N$
$S$
```
```
$N$
$X_1$ $Y_1$
$X_2$ $Y_2$
$\vdots$
$X_N$ $Y_N$
$S$
```
Output
If there will be a collision, print `Yes`; otherwise, print `No`.
Constraints
- $2 \leq N \leq 2 \times 10^5$
- $0 \leq X_i \leq 10^9$
- $0 \leq Y_i \leq 10^9$
- $(X_i, Y_i) \neq (X_j, Y_j)$ if $i \neq j$.
- All $X_i$ and $Y_i$ are integers.
- $S$ is a string of length $N$ consisting of `L` and `R`.
- $0 \leq X_i \leq 10^9$
- $0 \leq Y_i \leq 10^9$
- $(X_i, Y_i) \neq (X_j, Y_j)$ if $i \neq j$.
- All $X_i$ and $Y_i$ are integers.
- $S$ is a string of length $N$ consisting of `L` and `R`.
Sample 1 Input
3
2 3
1 1
4 1
RRL
Sample 1 Output
Yes
This input corresponds to the example in the Problem Statement.
If all people continue walking, Person 2 and Person 3 will collide. Thus, Yes should be printed.
If all people continue walking, Person 2 and Person 3 will collide. Thus, Yes should be printed.
Sample 2 Input
2
1 1
2 1
RR
Sample 2 Output
No
Since Person 1 and Person 2 walk in the same direction, they never collide.
Sample 3 Input
10
1 3
1 4
0 0
0 2
0 4
3 1
2 4
4 2
4 4
3 3
RLRRRLRLRR
Sample 3 Output
Yes