There is a skating rink represented by a grid with $H$ horizontal rows and $W$ vertical columns. Let $(i, j)$ denote the square at the $i$-th row from the top and $j$-th column from the left.

The skating rink has $N$ obstacles. The $i$-th obstacle is placed at $(X_i,Y_i)$.

In a single move, Takahashi chooses one of the four directions, up, down, left, or right, and keeps moving until he hits an obstacle.  
When he hits an obstacle, he stops at the square right before the obstacle. Since the skating rink is surrounded by cliffs, it is prohibited to start a move in which he will never hit an obstacle.

Takahashi is initially at $(s_x,s_y)$. He wants to make some number of moves to stop at $(g_x,g_y)$.

Find the minimum number of moves required to end up at $(g_x, g_y)$. If it is not possible, report the fact.

Input is given from Standard Input in the following format:

```
$H$ $W$ $N$
$s_x$ $s_y$
$g_x$ $g_y$
$X_1$ $Y_1$
$X_2$ $Y_2$
$\vdots$
$X_N$ $Y_N$
```

Print the minimum number of moves required to end up at $(g_x,g_y)$.  
If it is impossible to end up there, print `-1`.

-   $1\leq H \leq 10^9$
-   $1\leq W \leq 10^9$
-   $1\leq N \leq 10^5$
-   $1\leq s_x,g_x\leq H$
-   $1\leq s_y,g_y\leq W$
-   $1\leq X_i \leq H$
-   $1\leq Y_i \leq W$
-   $(s_x,s_y)\neq (g_x,g_y)$
-   $(s_x,s_y)\neq (X_i,Y_i)$
-   $(g_x,g_y)\neq (X_i,Y_i)$
-   If $i\neq j$, then $(X_i,Y_i)\neq (X_j,Y_j)$.
-   All values in input are integers.

4

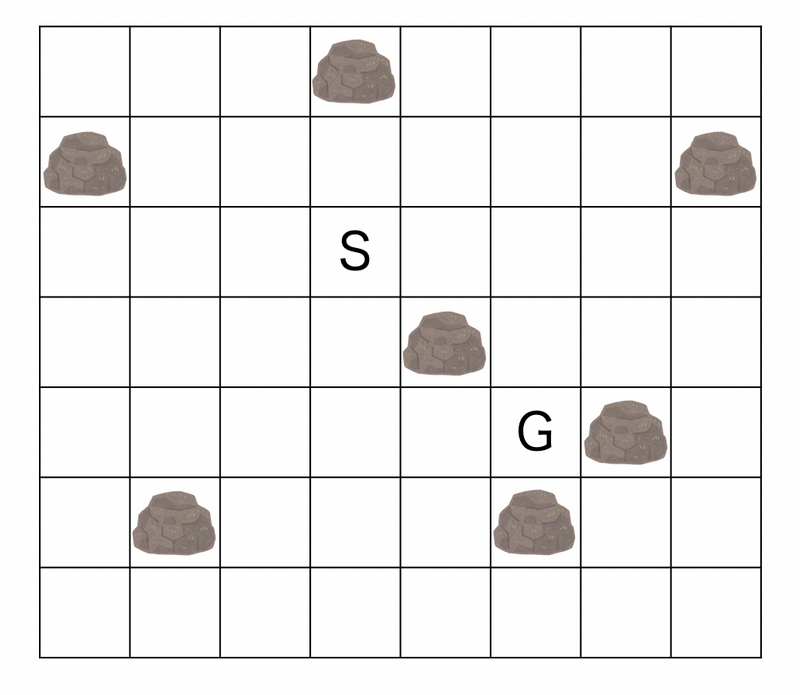
In the figure, $(s_x,s_y)$ is denoted by S and $(g_x,g_y)$ is denoted by G.
By moving as (3,4)→(2,4)→(2,2)→(5,2)→(5,6), he can end up at $(g_x,g_y)$ with 4 moves.

-1

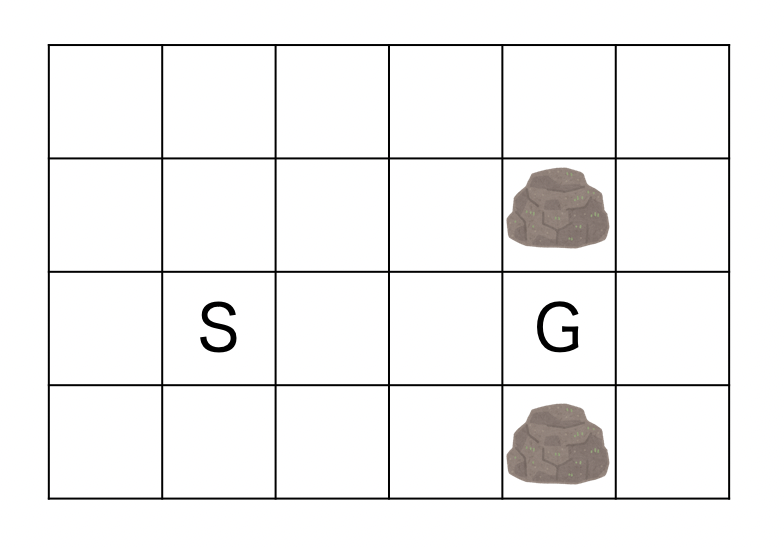
He must stop at $(g_x,g_y)$.
Note that just passing through $(g_x,g_y)$ is not considered to be ending up at the goal.

-1

If he chooses to move to the left, Takahashi will fall down the cliff after passing through $(g_x,g_y)$.
Note that it is prohibited to start a move in which he will never hit an obstacle, as the skating rink is surrounded by cliffs.