Takahashi has $N$ balls. Each ball has an integer not less than $2$ written on it. He will insert them in a cylinder one by one. The integer written on the $i$-th ball is $a_i$.

The balls are made of special material. When $k$ balls with $k$ $(k \geq 2)$ written on them line up in a row, all these $k$ balls will disappear.

For each $i$ $(1 \leq i \leq N)$, find the number of balls after inserting the $i$-th ball.

Input is given from Standard Input in the following format:

```
$N$
$a_1$ $\ldots$ $a_N$
```

Print $N$ lines. The $i$-th line $(1 \leq i \leq N)$ should contain the number of balls after inserting the $i$-th ball.

-   $1 \leq N \leq 2 \times 10^5$
-   $2 \leq a_i \leq 2 \times 10^5 \, (1 \leq i \leq N)$
-   All values in input are integers.

1
2
3
4
3

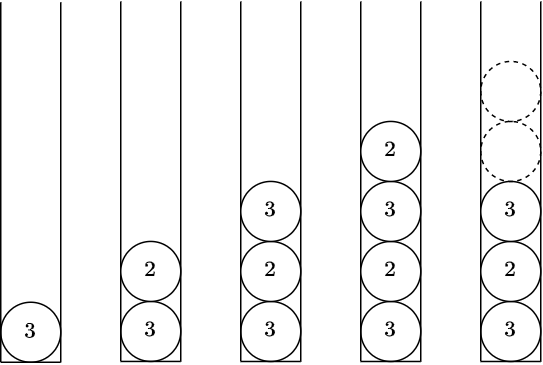
The content of the cylinder changes as follows.

• After inserting the 1-st ball, the cylinder contains the ball with 3.
• After inserting the 2-nd ball, the cylinder contains 3,2 from bottom to top.
• After inserting the 3-rd ball, the cylinder contains 3,2,3 from bottom to top.
• After inserting the 4-th ball, the cylinder contains 3,2,3,2 from bottom to top.
• After inserting the 5-th ball, the cylinder momentarily has 3,2,3,2,2 from bottom to top. The two consecutive balls with 22 disappear, and the cylinder eventually contains 3,2,3 from bottom to top.