We have a rooted tree with $N$ vertices. The vertices are numbered $1$ through $N$, and the root is Vertex $1$.  
The $i$-th edge connects Vertices $A_i$ and $B_i$.  
Vertex $i$ has an integer $X_i$ written on it.

You are given $Q$ queries. For the $i$-th query, given a pair of integers $(V_i,K_i)$, answer the following question.

-   Question: among the integers written on the vertices in the subtree rooted at Vertex $V_i$, find the $K_i$-th largest value.

Input is given from Standard Input in the following format:

```
$N$ $Q$
$X_1$ $\ldots$ $X_N$
$A_1$ $B_1$
$\vdots$
$A_{N-1}$ $B_{N-1}$
$V_1$ $K_1$
$\vdots$
$V_Q$ $K_Q$
```

Print $Q$ lines. The $i$-th line should contain the response to the $i$-th query.

-   $2 \leq N \leq 10^5$
-   $0\leq X_i\leq 10^9$
-   $1\leq A_i,B_i\leq N$
-   $1\leq Q \leq 10^5$
-   $1\leq V_i\leq N$
-   $1\leq K_i\leq 20$
-   The given graph is a tree.
-   The subtree rooted at Vertex $V_i$ has $K_i$ or more vertices.
-   All values in input are integers.

4
5

The tree given in this input is shown below.

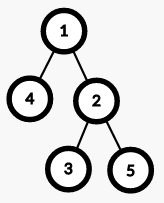
For the 1-st query, the vertices in the subtree rooted at Vertex 1 are Vertices 1,2,3,4, and 5, so print the 2-nd largest value of the numbers written on these vertices, 4.
For the 2-nd query, the vertices in the subtree rooted at Vertex 2 are Vertices 2,3, and 5, so print the 1-st largest value of the numbers written on these vertices, 5.