On an $xy$-coordinate plane, is there a lattice point whose distances from two lattice points $(x_1, y_1)$ and $(x_2, y_2)$ are both $\sqrt{5}$?

Notes
A point on an $xy$-coordinate plane whose $x$ and $y$ coordinates are both integers is called a lattice point.  
The distance between two points $(a, b)$ and $(c, d)$ is defined to be the Euclidean distance between them, $\sqrt{(a - c)^2 + (b-d)^2}$.

The following figure illustrates an $xy$-plane with a black circle at $(0, 0)$ and white circles at the lattice points whose distances from $(0, 0)$ are $\sqrt{5}$. (The grid shows where either $x$ or $y$ is an integer.)

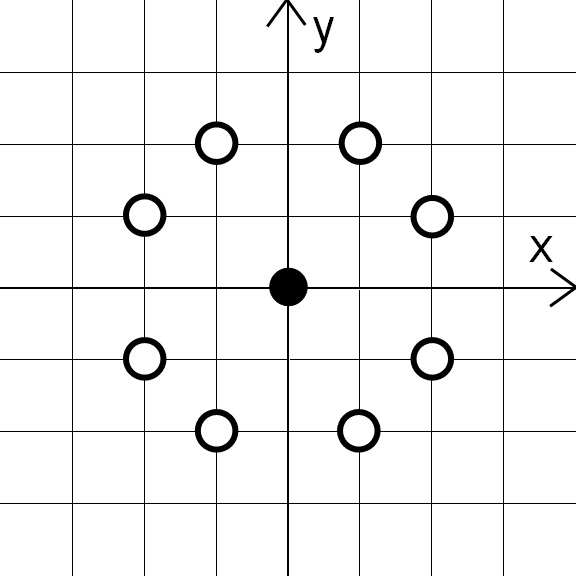
Input is given from Standard Input in the following format:

```
$x_1$ $y_1$ $x_2$ $y_2$
```

If there is a lattice point satisfying the condition, print `Yes`; otherwise, print `No`.

-   $-10^9 \leq x_1 \leq 10^9$
-   $-10^9 \leq y_1 \leq 10^9$
-   $-10^9 \leq x_2 \leq 10^9$
-   $-10^9 \leq y_2 \leq 10^9$
-   $(x_1, y_1) \neq (x_2, y_2)$
-   All values in input are integers.

Yes

• The distance between points (2,1) and (x1,y1) is $\sqrt{(0−2)^2+(0−1)^2}=5$;
• the distance between points (2,1) and (x2,y2) is $\sqrt{(3−2)^2+(3−1)^2}=5$;
• point (2,1) is a lattice point,

so point (2,1) satisfies the condition. Thus, Yes should be printed.
One can also assert in the same way that (1,2) also satisfies the condition.

No

No lattice point satisfies the condition, so No should be printed.

Yes

Point $(10^9+1,10^9−2)$ and point $(10^9−2,10^9+1)$ satisfy the condition.