9536: ABC222 —— H - Beautiful Binary Tree
[Creator : ]
Description
For a positive integer $N$, a rooted binary tree that satisfies the following conditions is said to be a beautiful binary tree of degree $N$.
- Each vertex has $0$ or $1$ written on it.
- Each vertex that is a leaf has $1$ written on it.
- It is possible to do the following operation at most $N-1$ times so that the root has $N$ written on it and the other vertices have $0$ written on them.
- Choose vertices $u$ and $v$, where $v$ must be a child of $u$ or a child of "a child of $u$." Let $a_u \gets a_u + a_v, a_v \gets 0$, where $a_u$ and $a_v$ are the numbers written on $u$ and $v$, respectively.
Given $N$, find the number, modulo $998244353$, of beautiful binary trees of degree $N$.
- Each vertex has $0$ or $1$ written on it.
- Each vertex that is a leaf has $1$ written on it.
- It is possible to do the following operation at most $N-1$ times so that the root has $N$ written on it and the other vertices have $0$ written on them.
- Choose vertices $u$ and $v$, where $v$ must be a child of $u$ or a child of "a child of $u$." Let $a_u \gets a_u + a_v, a_v \gets 0$, where $a_u$ and $a_v$ are the numbers written on $u$ and $v$, respectively.
Given $N$, find the number, modulo $998244353$, of beautiful binary trees of degree $N$.
Input
Input is given from Standard Input in the following format:
```
$N$
```
```
$N$
```
Output
Print the answer.
Constraints
- $1 \leq N \leq 10^7$
- All values in input are integers.
- All values in input are integers.
Sample 1 Input
1
Sample 1 Output
1
The only binary tree that satisfies the condition is a tree with one vertex whose root has 1 written on it.
Sample 2 Input
2
Sample 2 Output
6
The binary trees that satisfy the condition are the six trees shown below.
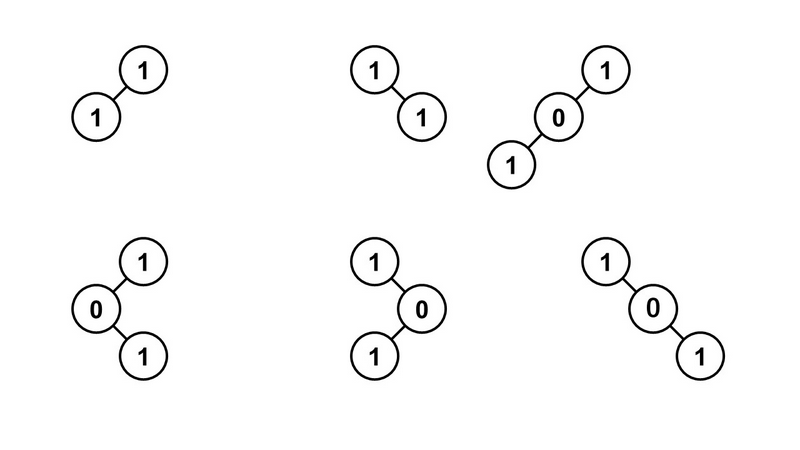
Sample 3 Input
222
Sample 3 Output
987355927
222222
675337738