Given are a tree with $N$ vertices, a sequence of $M$ numbers $A=(A_1,\ldots,A_M)$, and an integer $K$.  
The vertices are numbered $1$ through $N$, and the $i$-th edge connects Vertices $U_i$ and $V_i$.

We will paint each of the $N-1$ edges of this tree red or blue. Among the $2^{N-1}$ such ways, find the number of ones that satisfies the following condition, modulo $998244353$.

Condition:  
Let us put a piece on Vertex $A_1$, and for each $i=1,\ldots,M-1$ in this order, move it from Vertex $A_i$ to Vertex $A_{i+1}$ along the edges in the shortest path. After all of these movements, $R-B=K$ holds, where $R$ and $B$ are the numbers of times the piece traverses a red edge and a blue edge, respectively.

Input is given from Standard Input in the following format:

```
$N$ $M$ $K$
$A_1$ $A_2$ $\ldots$ $A_M$
$U_1$ $V_1$
$\vdots$
$U_{N-1}$ $V_{N-1}$
```

Print the answer.

-   $2 \leq N \leq 1000$
-   $2 \leq M \leq 100$
-   $|K| \leq 10^5$
-   $1 \leq A_i \leq N$
-   $1\leq U_i,V_i\leq N$
-   The given graph is a tree.
-   All values in input are integers.

2

If we paint the 1-st and 3-rd edges red and the 2-nd edge blue, the piece will traverse the following numbers of red and blue edges:

• 0 red edges and 1 blue edge when moving from Vertex 2 to 3,
• 0 red edges and 1 blue edge when moving from Vertex 3 to 2,
• 1 red edge and 0 blue edges when moving from Vertex 2 to 1,
• 2 red edges and 1 blue edge when moving from Vertex 1 to 4,

for a total of 3 red edges and 3 blue edges, satisfying the condition.

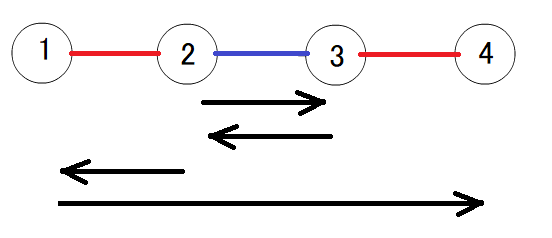
Another way to satisfy the condition is to paint the 1-st and 3-rd edges blue and the 2-nd edge red. There is no other way to satisfy it, so the answer is 2.

0

There may be no way to paint the tree to satisfy the condition.