9519: ABC220 —— G - Isosceles Trapezium
[Creator : ]
Description
In the $xy$-plane, we have $N$ points, each assigned a weight.
The $i$-th point has the coordinates $(X_i,Y_i)$ and the weight $C_i$.
We will choose four of the $N$ points to form an isosceles trapezoid whose vertices are the chosen points.
What is the maximum possible total weight of the points chosen here?
If it is impossible to form an isosceles trapezoid, print `-1`.
We remind you that an isosceles trapezoid is a quadrilateral that satisfies all of the following conditions.
- It is a trapezoid.
- For one of the two parallel sides, the two angles at its ends are equal.
The $i$-th point has the coordinates $(X_i,Y_i)$ and the weight $C_i$.
We will choose four of the $N$ points to form an isosceles trapezoid whose vertices are the chosen points.
What is the maximum possible total weight of the points chosen here?
If it is impossible to form an isosceles trapezoid, print `-1`.
We remind you that an isosceles trapezoid is a quadrilateral that satisfies all of the following conditions.
- It is a trapezoid.
- For one of the two parallel sides, the two angles at its ends are equal.
Input
Input is given from Standard Input in the following format:
```
$N$
$X_1$ $Y_1$ $C_1$
$X_2$ $Y_2$ $C_2$
$\vdots$
$X_N$ $Y_N$ $C_N$
```
```
$N$
$X_1$ $Y_1$ $C_1$
$X_2$ $Y_2$ $C_2$
$\vdots$
$X_N$ $Y_N$ $C_N$
```
Output
Print the answer.
Constraints
- $4 \leq N \leq 1000$
- $-10^9 \leq X_i,Y_i \leq 10^9$
- $1 \leq C_i \leq 10^9$
- $(X_i,Y_i) \neq (X_j,Y_j)$ if $i \neq j$.
- All values in input are integers.
- $-10^9 \leq X_i,Y_i \leq 10^9$
- $1 \leq C_i \leq 10^9$
- $(X_i,Y_i) \neq (X_j,Y_j)$ if $i \neq j$.
- All values in input are integers.
Sample 1 Input
5
0 3 10
3 3 10
-1 0 10
2 0 10000
4 0 10
Sample 1 Output
40
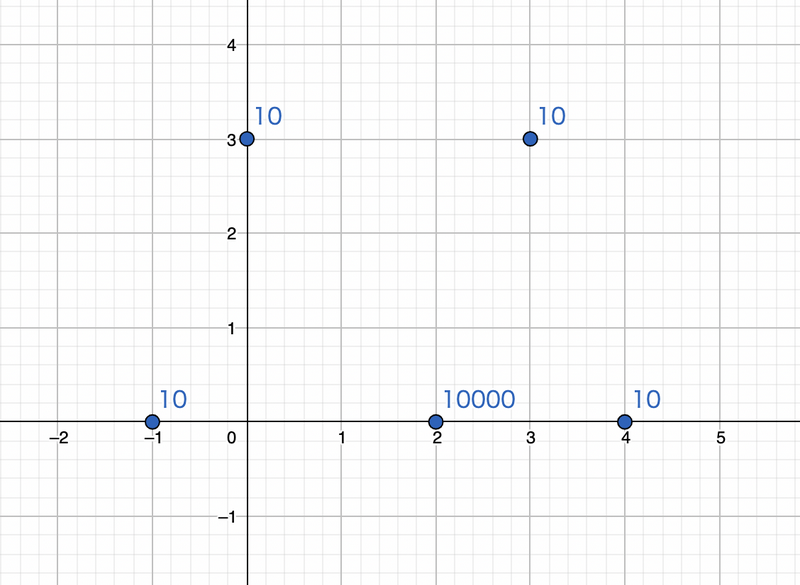
We can choose Points 1,2,3,5 to form an isosceles trapezoid, with the points having a total weight of 40.
Any other way to choose points would not form an isosceles trapezoid.
Sample 2 Input
6
0 1 1
1 4 20
2 7 300
5 6 4000
4 3 50000
3 0 600000
Sample 2 Output
650021
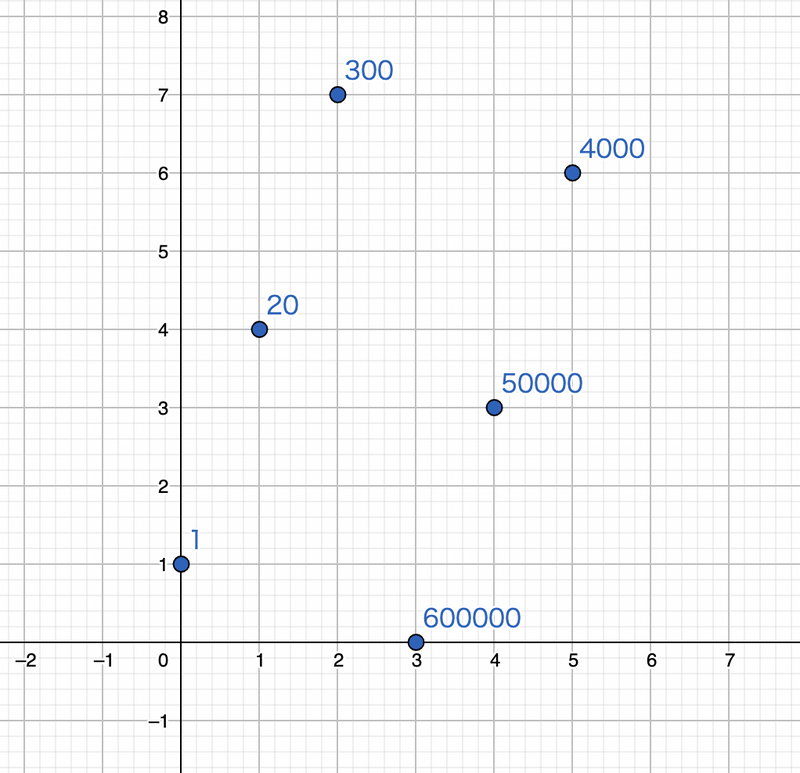
Note that a square and a rectangle are also isosceles trapezoids.
Sample 3 Input
7
-3 0 1
-2 0 1
-1 0 1
0 0 1
1 0 1
2 0 1
3 0 1
Sample 3 Output
-1
We cannot form an isosceles trapezoid.