We have a tree with $2^N-1$ vertices.  
The vertices are numbered $1$ through $2^N-1$. For each $1\leq i < 2^{N-1}$, the following edges exist:

-   an undirected edge connecting Vertex $i$ and Vertex $2i$,
-   an undirected edge connecting Vertex $i$ and Vertex $2i+1$.

There is no other edge.

Let the distance between two vertices be the number of edges in the simple path connecting those two vertices.

Find the number, modulo $998244353$, of pairs of vertices $(i, j)$ such that the distance between them is $D$.

Input is given from Standard Input in the following format:

```
$N$ $D$
```

Print the answer.

-   $2 \leq N \leq 10^6$
-   $1 \leq D \leq 2\times 10^6$
-   All values in input are integers.

14

The following figure describes the given tree.

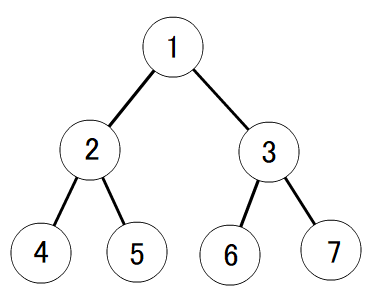
There are 14 pairs of vertices such that the distance between them is 2: (1,4),(1,5),(1,6),(1,7),(2,3),(3,2),(4,1),(4,5),(5,1),(5,4),(6,1),(6,7),(7,1),(7,6).