9511: ABC344 —— F - Earn to Advance
[Creator : ]
Description
There is a grid with $N$ rows and $N$ columns. Let $(i,j)$ denote the square at the $i$-th row from the top and $j$-th column from the left.
Takahashi is initially at square $(1,1)$ with zero money.
When Takahashi is at square $(i,j)$, he can perform one of the following in one action:
- Stay at the same square and increase his money by $P_{i,j}$.
- Pay $R_{i,j}$ from his money and move to square $(i,j+1)$.
- Pay $D_{i,j}$ from his money and move to square $(i+1,j)$.
He cannot make a move that would make his money negative or take him outside the grid.
If Takahashi acts optimally, how many actions does he need to reach square $(N,N)$?
Takahashi is initially at square $(1,1)$ with zero money.
When Takahashi is at square $(i,j)$, he can perform one of the following in one action:
- Stay at the same square and increase his money by $P_{i,j}$.
- Pay $R_{i,j}$ from his money and move to square $(i,j+1)$.
- Pay $D_{i,j}$ from his money and move to square $(i+1,j)$.
He cannot make a move that would make his money negative or take him outside the grid.
If Takahashi acts optimally, how many actions does he need to reach square $(N,N)$?
Input
The input is given from Standard Input in the following format:
```
$N$
$P_{1,1}$ $\ldots$ $P_{1,N}$
$\vdots$
$P_{N,1}$ $\ldots$ $P_{N,N}$
$R_{1,1}$ $\ldots$ $R_{1,N-1}$
$\vdots$
$R_{N,1}$ $\ldots$ $R_{N,N-1}$
$D_{1,1}$ $\ldots$ $D_{1,N}$
$\vdots$
$D_{N-1,1}$ $\ldots$ $D_{N-1,N}$
```
```
$N$
$P_{1,1}$ $\ldots$ $P_{1,N}$
$\vdots$
$P_{N,1}$ $\ldots$ $P_{N,N}$
$R_{1,1}$ $\ldots$ $R_{1,N-1}$
$\vdots$
$R_{N,1}$ $\ldots$ $R_{N,N-1}$
$D_{1,1}$ $\ldots$ $D_{1,N}$
$\vdots$
$D_{N-1,1}$ $\ldots$ $D_{N-1,N}$
```
Output
Print the answer.
Constraints
- $2 \leq N \leq 80$
- $1 \leq P_{i,j} \leq 10^9$
- $1 \leq R_{i,j},D_{i,j} \leq 10^9$
- All input values are integers.
- $1 \leq P_{i,j} \leq 10^9$
- $1 \leq R_{i,j},D_{i,j} \leq 10^9$
- All input values are integers.
Sample 1 Input
3
1 2 3
3 1 2
2 1 1
1 2
4 3
4 2
1 5 7
5 3 3
Sample 1 Output
8
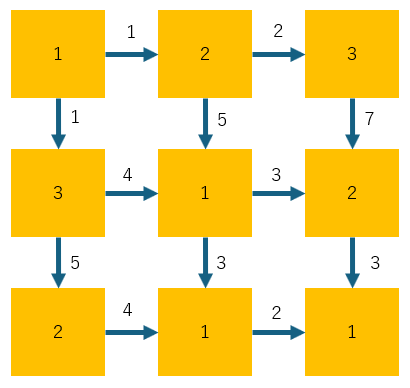
It is possible to reach square (3,3) in eight actions as follows:
- Stay at square (1,1) and increase money by 1. His money is now 1.
- Pay 1 money and move to square (2,1). His money is now 0.
- Stay at square (2,1) and increase money by 3. His money is now 3.
- Stay at square (2,1) and increase money by 3. His money is now 6.
- Stay at square (2,1) and increase money by 3. His money is now 9.
- Pay 4 money and move to square (2,2). His money is now 5.
- Pay 3 money and move to square (3,2). His money is now 2.
- Pay 2 money and move to square (3,3). His money is now 0.
Sample 2 Input
3
1 1 1
1 1 1
1 1 1
1000000000 1000000000
1000000000 1000000000
1000000000 1000000000
1000000000 1000000000 1000000000
1000000000 1000000000 1000000000
Sample 2 Output
4000000004