9502: ABC219 —— E - Moat
[Creator : ]
Description
There are villages at some number of points in the $xy$-plane.
Takahashi will construct a moat to protect these villages from enemies such as civil armies and witches.
You are given a $4 \times 4$ matrix $A = (A_{i, j})$ consisting of $0$ and $1$.
For each pair of integers $(i, j)$ $(1 \leq i, j \leq 4)$ such that $A_{i, j} = 1$, there is a village at the coordinates $(i-0.5, j-0.5)$.
The moat will be a polygon in the plane. Takahashi will construct it so that the following conditions will be satisfied. (See also the annotation at Sample Input/Output 1.)
1. There is no self-intersection.
2. All villages are contained in the interior of the polygon.
3. The $x$- and $y$-coordinates of every vertex are integers between $0$ and $4$ (inclusive).
4. Every edge is parallel to the $x$- or $y$-axis.
5. Every inner angle is $90$ or $270$ degrees.
Print the number of ways in which Takahashi can construct the moat.
Takahashi will construct a moat to protect these villages from enemies such as civil armies and witches.
You are given a $4 \times 4$ matrix $A = (A_{i, j})$ consisting of $0$ and $1$.
For each pair of integers $(i, j)$ $(1 \leq i, j \leq 4)$ such that $A_{i, j} = 1$, there is a village at the coordinates $(i-0.5, j-0.5)$.
The moat will be a polygon in the plane. Takahashi will construct it so that the following conditions will be satisfied. (See also the annotation at Sample Input/Output 1.)
1. There is no self-intersection.
2. All villages are contained in the interior of the polygon.
3. The $x$- and $y$-coordinates of every vertex are integers between $0$ and $4$ (inclusive).
4. Every edge is parallel to the $x$- or $y$-axis.
5. Every inner angle is $90$ or $270$ degrees.
Print the number of ways in which Takahashi can construct the moat.
Input
Input is given from Standard Input in the following format:
```
$A_{1, 1}$ $A_{1, 2}$ $A_{1, 3}$ $A_{1, 4}$
$A_{2, 1}$ $A_{2, 2}$ $A_{2, 3}$ $A_{2, 4}$
$A_{3, 1}$ $A_{3, 2}$ $A_{3, 3}$ $A_{3, 4}$
$A_{4, 1}$ $A_{4, 2}$ $A_{4, 3}$ $A_{4, 4}$
```
```
$A_{1, 1}$ $A_{1, 2}$ $A_{1, 3}$ $A_{1, 4}$
$A_{2, 1}$ $A_{2, 2}$ $A_{2, 3}$ $A_{2, 4}$
$A_{3, 1}$ $A_{3, 2}$ $A_{3, 3}$ $A_{3, 4}$
$A_{4, 1}$ $A_{4, 2}$ $A_{4, 3}$ $A_{4, 4}$
```
Output
Print the number of ways in which Takahashi can construct the moat.
Constraints
- $A_{i, j} \in \lbrace 0, 1\rbrace$
- There is at least one pair $(i, j)$ such that $A_{i, j} = 1$.
- There is at least one pair $(i, j)$ such that $A_{i, j} = 1$.
Sample 1 Input
1 0 0 0
0 0 1 0
0 0 0 0
1 0 0 0
Sample 1 Output
1272
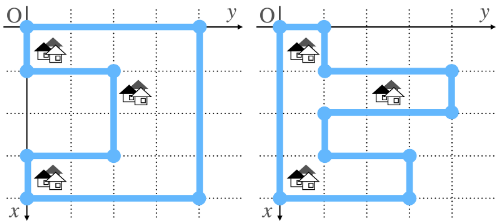
The two ways to construct the moat shown in the images below are valid.
The four ways to construct the moat shown in the images below are invalid.
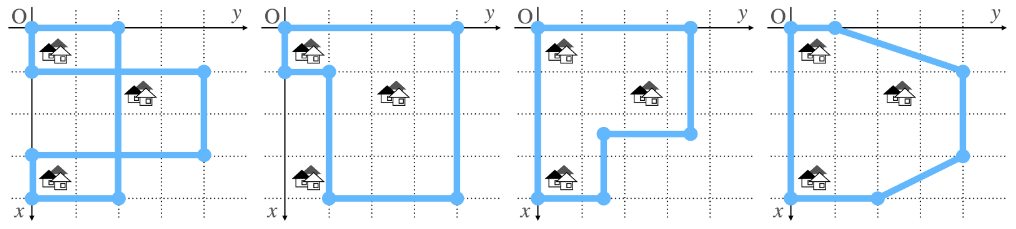
Here are the reasons the above ways are invalid.

The four ways to construct the moat shown in the images below are invalid.

Here are the reasons the above ways are invalid.
- The first way violates the condition: "There is no self-intersection."
- The second way violates the condition: "All villages are contained in the interior of the polygon."
- The third way violates the condition: "The x- and y-coordinates of every vertex are integers between 00 and 44." (Some vertices have non-integer coordinates.)
- The fourth way violates the condition: "Every edge is parallel to the x- or y-axis."
Sample 2 Input
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
Sample 2 Output
1