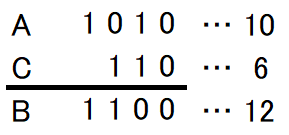9434: ABC213 —— A - Bitwise Exclusive Or
[Creator : ]
Description
You are given integers $A$ and $B$ between $0$ and $255$ (inclusive). Find a non-negative integer $C$ such that $A \text{ xor }C=B$.
It can be proved that there uniquely exists such $C$, and it will be between $0$ and $255$ (inclusive).
What is bitwise $\mathrm{XOR}$?
The bitwise $\mathrm{XOR}$ of integers $A$ and $B$, $A\ \mathrm{XOR}\ B$, is defined as follows:
- When $A\ \mathrm{XOR}\ B$ is written in base two, the digit in the $2^k$'s place ($k \geq 0$) is $1$ if exactly one of $A$ and $B$ is $1$, and $0$ otherwise.
For example, we have $3\ \mathrm{XOR}\ 5 = 6$ (in base two: $011\ \mathrm{XOR}\ 101 = 110$).
It can be proved that there uniquely exists such $C$, and it will be between $0$ and $255$ (inclusive).
What is bitwise $\mathrm{XOR}$?
The bitwise $\mathrm{XOR}$ of integers $A$ and $B$, $A\ \mathrm{XOR}\ B$, is defined as follows:
- When $A\ \mathrm{XOR}\ B$ is written in base two, the digit in the $2^k$'s place ($k \geq 0$) is $1$ if exactly one of $A$ and $B$ is $1$, and $0$ otherwise.
For example, we have $3\ \mathrm{XOR}\ 5 = 6$ (in base two: $011\ \mathrm{XOR}\ 101 = 110$).
Input
Input is given from Standard Input in the following format:
```
$A$ $B$
```
```
$A$ $B$
```
Output
Print the answer.
Constraints
- $0\leq A,B \leq 255$
- All values in input are integers.
- All values in input are integers.
Sample 1 Input
3 6
Sample 1 Output
5
When written in binary, 3 will be 11, and 5 will be 101. Thus, their xorxor will be 110 in binary, or 6 in decimal.
In short, 3 xor 5=6, so the answer is 5.
In short, 3 xor 5=6, so the answer is 5.
Sample 2 Input
10 12
Sample 2 Output
6