9430: ABC211 —— F - Rectilinear Polygons
[Creator : ]
Description
We have $N$ polygons on the $xy$-plane.
Every side of these polygons is parallel to the $x$- or $y$-axis, and every interior angle is $90$ or $270$ degrees. All of these polygons are simple.
The $i$-th polygon has $M_i$ corners, the $j$-th of which is $(x_{i, j}, y_{i, j})$.
The sides of this polygon are segments connecting the $j$-th and $(j+1)$-th corners. (Assume that $(M_i+1)$-th corner is the $1$-st corner.)
A polygon is simple when...
for any two of its sides that are not adjacent, they do not intersect (cross or touch) each other.
You are given $Q$ queries. For each $i = 1, 2, \dots, Q$, the $i$-th query is as follows.
- Among the $N$ polygons, how many have the point $(X_i + 0.5, Y_i + 0.5)$ inside them?
Every side of these polygons is parallel to the $x$- or $y$-axis, and every interior angle is $90$ or $270$ degrees. All of these polygons are simple.
The $i$-th polygon has $M_i$ corners, the $j$-th of which is $(x_{i, j}, y_{i, j})$.
The sides of this polygon are segments connecting the $j$-th and $(j+1)$-th corners. (Assume that $(M_i+1)$-th corner is the $1$-st corner.)
A polygon is simple when...
for any two of its sides that are not adjacent, they do not intersect (cross or touch) each other.
You are given $Q$ queries. For each $i = 1, 2, \dots, Q$, the $i$-th query is as follows.
- Among the $N$ polygons, how many have the point $(X_i + 0.5, Y_i + 0.5)$ inside them?
Input
Input is given from Standard Input in the following format:
```
$N$
$M_1$
$x_{1, 1}$ $y_{1, 1}$ $x_{1, 2}$ $y_{1, 2}$ $\dots$ $x_{1, M_1}$ $y_{1, M_1}$
$M_2$
$x_{2, 1}$ $y_{2, 1}$ $x_{2, 2}$ $y_{2, 2}$ $\dots$ $x_{2, M_2}$ $y_{2, M_2}$
$\vdots$
$M_N$
$x_{N, 1}$ $y_{N, 1}$ $x_{N, 2}$ $y_{N, 2}$ $\dots$ $x_{N, M_N}$ $y_{N, M_N}$
$Q$
$X_1$ $Y_1$
$X_2$ $Y_2$
$\vdots$
$X_Q$ $Y_Q$
```
```
$N$
$M_1$
$x_{1, 1}$ $y_{1, 1}$ $x_{1, 2}$ $y_{1, 2}$ $\dots$ $x_{1, M_1}$ $y_{1, M_1}$
$M_2$
$x_{2, 1}$ $y_{2, 1}$ $x_{2, 2}$ $y_{2, 2}$ $\dots$ $x_{2, M_2}$ $y_{2, M_2}$
$\vdots$
$M_N$
$x_{N, 1}$ $y_{N, 1}$ $x_{N, 2}$ $y_{N, 2}$ $\dots$ $x_{N, M_N}$ $y_{N, M_N}$
$Q$
$X_1$ $Y_1$
$X_2$ $Y_2$
$\vdots$
$X_Q$ $Y_Q$
```
Output
Print $Q$ lines.
The $i$-th line should contain the answer to the $i$-th query.
The $i$-th line should contain the answer to the $i$-th query.
Constraints
- $1 \leq N \leq 10^5$
- $4 \leq M_i \leq 10^5$
- Each $M_i$ is even.
- $\sum_i M_i \leq 4 \times 10^5$
- $0 \leq x_{i, j}, y_{i, j} \leq 10^5$
- $(x_{i, j}, y_{i, j}) \neq (x_{i, k}, y_{i, k})$ if $j \neq k$.
- $x_{i, j} = x_{i, j+1}$ for $j = 1, 3, \dots M_i-1$.
- $y_{i, j} = y_{i, j+1}$ for $j = 2, 4, \dots M_i$. (Assume $y_{i, M_i +1} = y_{i, 1}$.)
- The given polygons are simple.
- $1 \leq Q \leq 10^5$
- $0 \leq X_i, Y_i \lt 10^5$
- All values in input are integers.
- $4 \leq M_i \leq 10^5$
- Each $M_i$ is even.
- $\sum_i M_i \leq 4 \times 10^5$
- $0 \leq x_{i, j}, y_{i, j} \leq 10^5$
- $(x_{i, j}, y_{i, j}) \neq (x_{i, k}, y_{i, k})$ if $j \neq k$.
- $x_{i, j} = x_{i, j+1}$ for $j = 1, 3, \dots M_i-1$.
- $y_{i, j} = y_{i, j+1}$ for $j = 2, 4, \dots M_i$. (Assume $y_{i, M_i +1} = y_{i, 1}$.)
- The given polygons are simple.
- $1 \leq Q \leq 10^5$
- $0 \leq X_i, Y_i \lt 10^5$
- All values in input are integers.
Sample 1 Input
3
4
1 2 1 4 3 4 3 2
4
2 5 2 3 5 3 5 5
4
5 6 5 5 3 5 3 6
3
1 4
2 3
4 5
Sample 1 Output
0
2
1
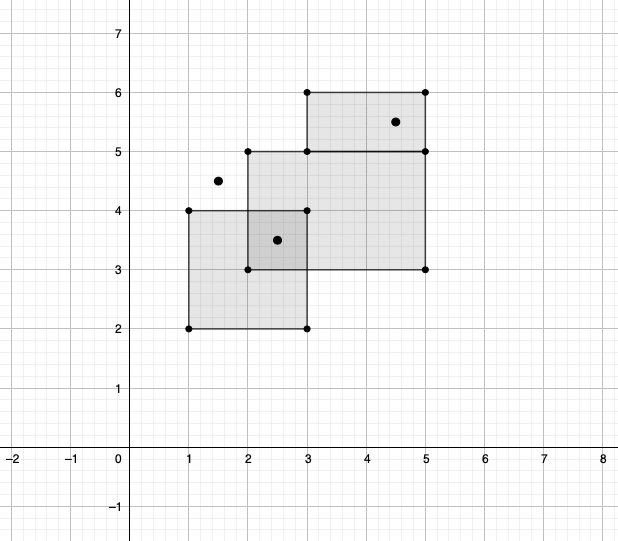
Note that different polygons may cross or touch each other.
Sample 2 Input
2
4
12 3 12 5 0 5 0 3
12
1 1 1 9 10 9 10 0 4 0 4 6 6 6 6 2 8 2 8 7 2 7 2 1
4
2 6
4 4
6 3
1 8
Sample 2 Output
0
2
1
1
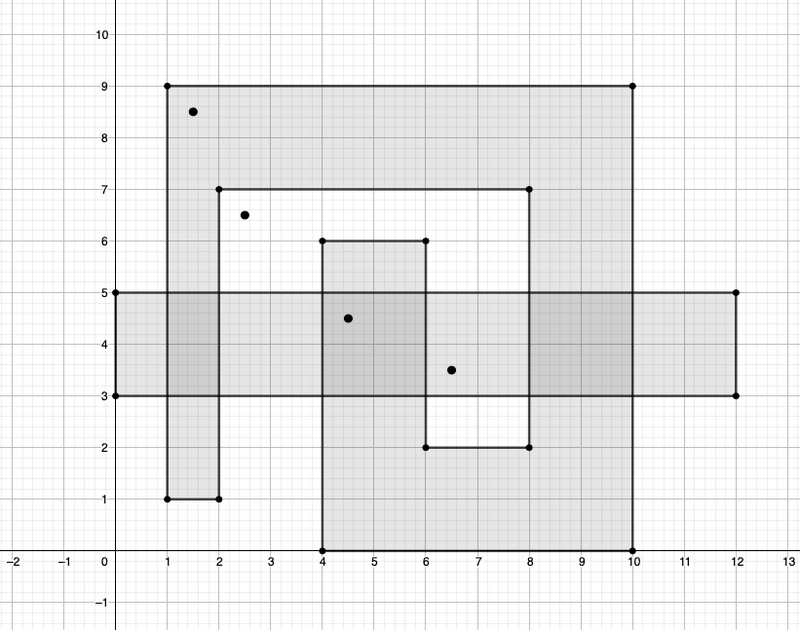
Although the polygons are simple, they may not be convex.