There is a convex $N$-gon $S$ in the two-dimensional coordinate plane where the positive $x$-axis points to the right and the positive $y$-axis points upward. The vertices of $S$ have the coordinates $(X_1,Y_1),\ldots,(X_N,Y_N)$ in counter-clockwise order.

For each of $Q$ points $(A_i,B_i)$, answer the following question: is that point inside or outside or on the boundary of $S$?

The input is given from Standard Input in the following format:

```
$N$
$X_1$ $Y_1$
$\vdots$
$X_N$ $Y_N$
$Q$
$A_1$ $B_1$
$\vdots$
$A_Q$ $B_Q$
```

Print $Q$ lines. The $i$-th line should contain `IN` if $(A_i,B_i)$ is inside $S$ (and not on the boundary), `OUT` if it is outside $S$ (and not on the boundary), and `ON` if it is on the boundary of $S$.

-   $3 \leq N \leq 2\times 10^5$
-   $1 \leq Q \leq 2\times 10^5$
-   $-10^9 \leq X_i,Y_i,A_i,B_i \leq 10^9$
-   $S$ is a strictly convex $N$-gon. That is, its interior angles are all less than $180$ degrees.
-   $(X_1,Y_1),\ldots,(X_N,Y_N)$ are the vertices of $S$ in counter-clockwise order.
-   All values in the input are integers.

ON
IN
OUT

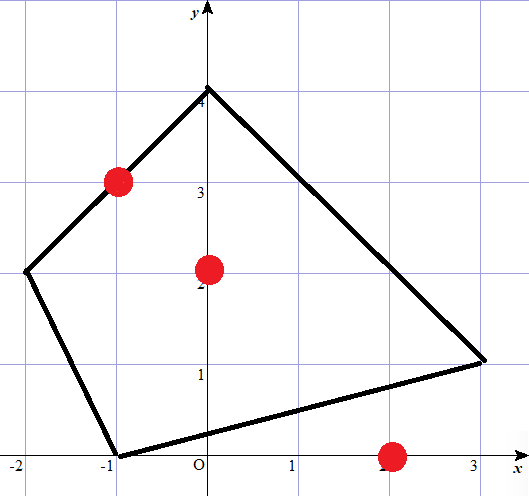
The figure below shows S and the given three points. The first point is on the boundary of S, the second is inside S, and the third is outside S.