在数轴上有 $n$ 个闭区间从 $1$ 至 $n$ 编号，第 $i$ 个闭区间为 $[l_i,r_i]$ 。
现在要从中选出 $m$ 个区间，使得这 $m$ 个区间共同包含至少一个位置。换句话说，就是使得存在一个 $x$ ，使得对于每一个被选中的区间 $[l_i,r_i]$，都有 $l_i \leq x \leq r_i$ 。
对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。
区间 $[l_i,r_i]$ 的长度定义为 $(r_i-l_i)$ ，即等于它的右端点的值减去左端点的值。
求所有合法方案中最小的花费。如果不存在合法的方案，输出 $-1$。

第一行包含两个整数，分别代表 $n$ 和 $m$。
第 $2$ 到第 $(n + 1)$ 行，每行两个整数表示一个区间，第 $(i + 1)$ 行的整数 $l_i, r_i$ 分别代表第 $i$ 个区间的左右端点。

输出一行一个整数表示答案。

对于全部的测试点，保证 $1 \leq m \leq n$，$1 \leq n \leq 5 \times 10^5$，$1 \leq m \leq 2 \times 10^5$，$0 \leq l_i \leq r_i \leq 10^9$。

2

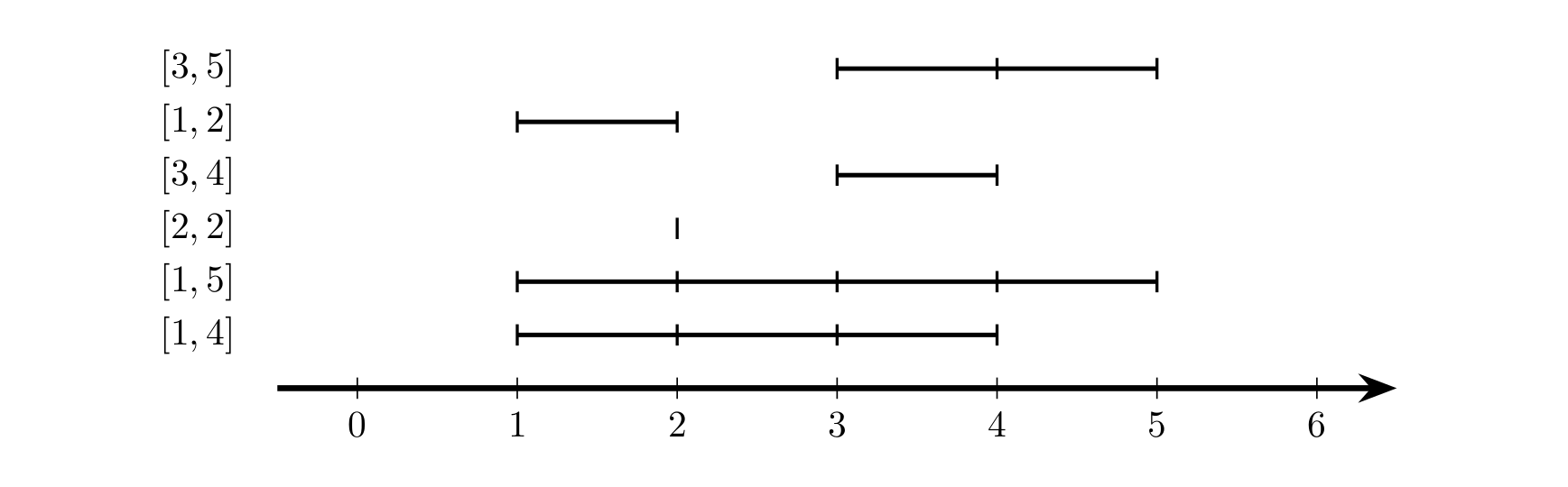
 如图，当 $n=6$，$m=3$ 时，花费最小的方案是选取 $[3,5],[3,4],[1,4]$ 这三个区间，它们共同包含了 $4$ 这个位置，所以是合法的。其中最长的区间是 $[1, 4]$，最短的区间是 $[3, 4]$，所以它的花费是 $(4 - 1) - (4 - 3) = 2$。