Allison 最近迷上了文学。她喜欢在一个慵懒的午后，细细地品上一杯卡布奇诺，静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》 组成的鸿篇巨制《荷马史诗》实在是太长了，Allison 想通过一种编码方式使得它变得短一些。

一部《荷马史诗》中有 $n$ 种不同的单词，从 $1$ 到 $n$ 进行编号。其中第 $i$ 种单词出现的总次数为 $w_i$。Allison 想要用 $k$ 进制串 $s_i$ 来替换第 $i$ 种单词，使得其满足如下要求：

对于任意的 $1\leq i, j\leq n$ ，$i\ne j$ ，都有：$s_i$ 不是 $s_j$ 的前缀。

现在 Allison 想要知道，如何选择 $s_i$，才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下，Allison 还想知道最长的 $s_i$ 的最短长度是多少？

一个字符串被称为 $k$ 进制字符串，当且仅当它的每个字符是 $0$ 到 $k-1$ 之间（包括 $0$ 和 $k-1$ ）的整数。

字符串 $str1$ 被称为字符串 $str2$ 的前缀，当且仅当：存在 $1 \leq t\leq m$ ，使得 $str1 = str2[1..t]$。其中，$m$ 是字符串 $str2$ 的长度，$str2[1..t]$ 表示 $str2$ 的前 $t$ 个字符组成的字符串。

输入的第 $1$ 行包含 $2$ 个正整数 $n, k$ ，中间用单个空格隔开，表示共有 $n$ 种单词，需要使用 $k$ 进制字符串进行替换。

接下来 $n$ 行，第 $i + 1$ 行包含 $1$ 个非负整数 $w_i$，表示第 $i$ 种单词的出现次数。

输出包括 $2$ 行。

第 $1$ 行输出 $1$ 个整数，为《荷马史诗》经过重新编码以后的最短长度。

第 $2$ 行输出 $1$ 个整数，为保证最短总长度的情况下，最长字符串 $s_i$ 的最短长度。

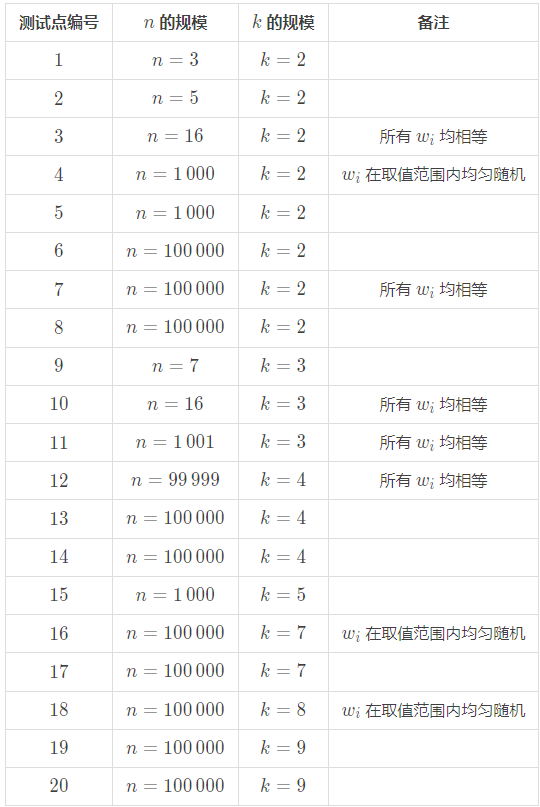
所有测试数据的范围和特点如下表所示（所有数据均满足 $0 < w_i \leq 10^{11}$）：

12
2

用 $X(k)$ 表示 $X$ 是以 $k$ 进制表示的字符串。
一种最优方案：令 $00(2)$ 替换第 $1$ 种单词， $01(2)$ 替换第 2 种单词， $10(2)$ 替换第 $3$ 种单词，$11(2)$ 替换第 $4$ 种单词。在这种方案下，编码以后的最短长度为：
$1 × 2 + 1 × 2 + 2 × 2 + 2 × 2 = 12$
最长字符串 $s_i$ 的长度为 $2$ 。
一种非最优方案：令 $000(2)$ 替换第 $1$ 种单词，$001(2)$ 替换第 $2$ 种单词，$01(2)$ 替换第 $3$ 种单词，$1(2)$ 替换第 $4$ 种单词。在这种方案下，编码以后的最短长度为：
$1 × 3 + 1 × 3 + 2 × 2 + 2 × 1 = 12$
最长字符串 $s_i$ 的长度为 $3$ 。与最优方案相比，文章的长度相同，但是最长字符串的长度更长一些。

36
3

一种最优方案：令 $000(3)$ 替换第 $1$ 种单词，$001(3)$ 替换第 $2$ 种单词，$01(3)$ 替换第 $3$ 种单词， $02(3)$ 替换第 $4$ 种单词， $1(3)$ 替换第 5 种单词， $2(3)$ 替换第 $6$ 种单词。