9267: ABC295 —— B - Bombs
[Creator : ]
Description
### Problem Statement
We have a board with $R$ rows running horizontally and $C$ columns running vertically. Let $(i,j)$ denote the square at the $i$-th row from the top and $j$-th column from the left.
You are given characters $B_{i,j}$ representing the current states of $(i,j)$. `.` represents an empty square; `#` represents a square with a wall; `1`, `2`,$\dots$, `9` represent a square with a bomb of power $1,2,\dots,9$, respectively.
At the next moment, all bombs will explode **simultaneously**. When a bomb explodes, every square whose Manhattan distance from the square with the bomb is not greater than the power of the bomb will turn into an empty square. Here, the Manhattan distance from $(r_1,c_1)$ to $(r_2,c_2)$ is $|r_1-r_2|+|c_1-c_2|$.
Print the board after the explosions.
We have a board with $R$ rows running horizontally and $C$ columns running vertically. Let $(i,j)$ denote the square at the $i$-th row from the top and $j$-th column from the left.
You are given characters $B_{i,j}$ representing the current states of $(i,j)$. `.` represents an empty square; `#` represents a square with a wall; `1`, `2`,$\dots$, `9` represent a square with a bomb of power $1,2,\dots,9$, respectively.
At the next moment, all bombs will explode **simultaneously**. When a bomb explodes, every square whose Manhattan distance from the square with the bomb is not greater than the power of the bomb will turn into an empty square. Here, the Manhattan distance from $(r_1,c_1)$ to $(r_2,c_2)$ is $|r_1-r_2|+|c_1-c_2|$.
Print the board after the explosions.
Input
### Input
The input is given from Standard Input in the following format:
```
$R$ $C$
$B_{1,1}B_{1,2}\dots B_{1,C}$
$\vdots$
$B_{R,1}B_{R,2}\dots B_{R,C}$
```
The input is given from Standard Input in the following format:
```
$R$ $C$
$B_{1,1}B_{1,2}\dots B_{1,C}$
$\vdots$
$B_{R,1}B_{R,2}\dots B_{R,C}$
```
Output
### Output
Print $R$ lines representing the board after the explosions. Use the format used in the input (do not print $R$ or $C$).
Print $R$ lines representing the board after the explosions. Use the format used in the input (do not print $R$ or $C$).
Constraints
### Constraints
- $1\leq R,C \leq 20$
- $R$ and $C$ are integers.
- Each $B_{i,j}$ is one of `.`, `#`, `1`, `2`, $\dots$, `9`.
- $1\leq R,C \leq 20$
- $R$ and $C$ are integers.
- Each $B_{i,j}$ is one of `.`, `#`, `1`, `2`, $\dots$, `9`.
Sample 1 Input
4 4
.1.#
###.
.#2.
#.##
Sample 1 Output
...#
#...
....
#...
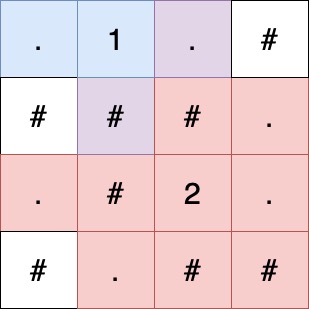
- The explosion of the bomb at (1,2) will turn the blue squares and purple squares in the above figure into empty squares.
- The explosion of the bomb at (3,3) will turn the red squares and purple squares in the above figure into empty squares.
Sample 2 Input
2 5
..#.#
###.#
Sample 2 Output
..#.#
###.#
Sample 3 Input
2 3
11#
###
Sample 3 Output
...
..#
4 6
#.#3#.
###.#.
##.###
#1..#.
......
#.....
#....#
....#.