9264: ABC294 —— G - Distance Queries on a Tree
[Creator : ]
Description
### Problem Statement
You are given a tree $T$ with $N$ vertices. Edge $i$ $(1\leq i\leq N-1)$ connects vertices $u _ i$ and $v _ i$, and has a weight of $w _ i$.
Process $Q$ queries in order. There are two kinds of queries as follows.
- `1 i w` : Change the weight of edge $i$ to $w$.
- `2 u v`:Print the distance between vertex $u$ and vertex $v$.
Here, the distance between two vertices $u$ and $v$ of a tree is the smallest total weight of edges in a path whose endpoints are $u$ and $v$.
You are given a tree $T$ with $N$ vertices. Edge $i$ $(1\leq i\leq N-1)$ connects vertices $u _ i$ and $v _ i$, and has a weight of $w _ i$.
Process $Q$ queries in order. There are two kinds of queries as follows.
- `1 i w` : Change the weight of edge $i$ to $w$.
- `2 u v`:Print the distance between vertex $u$ and vertex $v$.
Here, the distance between two vertices $u$ and $v$ of a tree is the smallest total weight of edges in a path whose endpoints are $u$ and $v$.
Input
### Input
The input is given from Standard Input in the following format:
```
$N$
$u _ 1$ $v _ 1$ $w _ 1$
$u _ 2$ $v _ 2$ $w _ 2$
$\vdots$
$u _ {N-1}$ $v _ {N-1}$ $w _ {N-1}$
$Q$
$\operatorname{query} _ 1$
$\operatorname{query} _ 2$
$\vdots$
$\operatorname{query} _ Q$
```
Here, $\operatorname{query} _ i$ denotes the $i$\-th query and is in one of the following format:
```
$1$ $i$ $w$
```
```
$2$ $u$ $v$
```
The input is given from Standard Input in the following format:
```
$N$
$u _ 1$ $v _ 1$ $w _ 1$
$u _ 2$ $v _ 2$ $w _ 2$
$\vdots$
$u _ {N-1}$ $v _ {N-1}$ $w _ {N-1}$
$Q$
$\operatorname{query} _ 1$
$\operatorname{query} _ 2$
$\vdots$
$\operatorname{query} _ Q$
```
Here, $\operatorname{query} _ i$ denotes the $i$\-th query and is in one of the following format:
```
$1$ $i$ $w$
```
```
$2$ $u$ $v$
```
Output
### Output
Print $q$ lines, where $q$ is the number of queries of the second kind. The $j$-th line $(1\leq j\leq q)$ should contain the answer to the $j$-th query of the second kind.
Print $q$ lines, where $q$ is the number of queries of the second kind. The $j$-th line $(1\leq j\leq q)$ should contain the answer to the $j$-th query of the second kind.
Constraints
### Constraints
- $1\leq N\leq 2\times10^5$
- $1\leq u _ i,v _ i\leq N\ (1\leq i\leq N-1)$
- $1\leq w _ i\leq 10^9\ (1\leq i\leq N-1)$
- The given graph is a tree.
- $1\leq Q\leq 2\times10^5$
- For each query of the first kind,
- $1\leq i\leq N-1$, and
- $1\leq w\leq 10^9$.
- For each query of the second kind,
- $1\leq u,v\leq N$.
- There is at least one query of the second kind.
- All values in the input are integers.
- $1\leq N\leq 2\times10^5$
- $1\leq u _ i,v _ i\leq N\ (1\leq i\leq N-1)$
- $1\leq w _ i\leq 10^9\ (1\leq i\leq N-1)$
- The given graph is a tree.
- $1\leq Q\leq 2\times10^5$
- For each query of the first kind,
- $1\leq i\leq N-1$, and
- $1\leq w\leq 10^9$.
- For each query of the second kind,
- $1\leq u,v\leq N$.
- There is at least one query of the second kind.
- All values in the input are integers.
Sample 1 Input
5
1 2 3
1 3 6
1 4 9
4 5 10
4
2 2 3
2 1 5
1 3 1
2 1 5
Sample 1 Output
9
19
11
The initial tree is shown in the figure below.
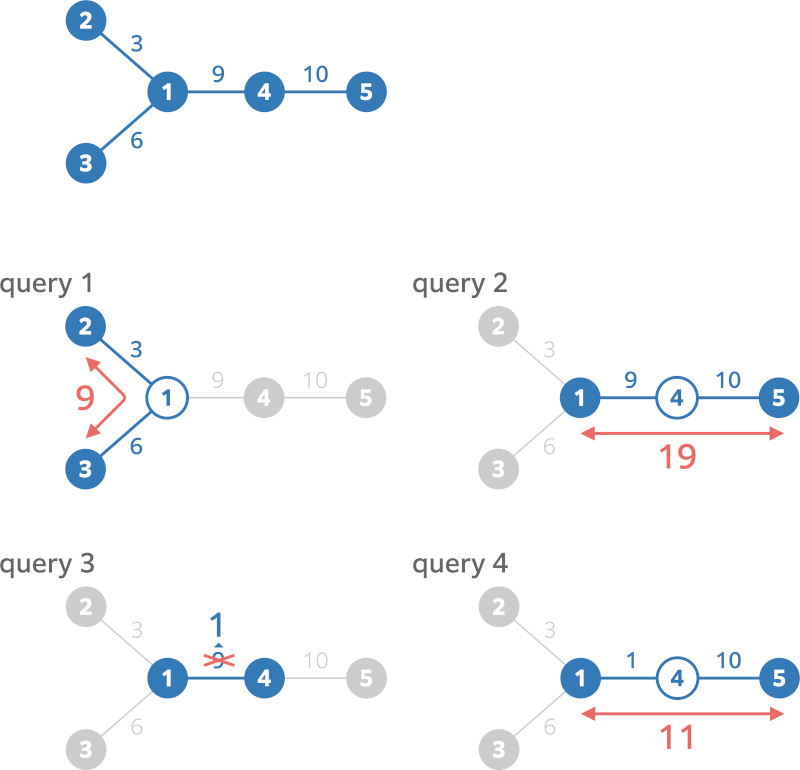
Each query should be processed as follows.

Each query should be processed as follows.
- The first query asks you to print the distance between vertex 2 and vertex 3. Edge 1 and edge 2, in this order, form a path between them with a total weight of 9, which is the minimum, so you should print 9.
- The second query asks you to print the distance between vertex 1 and vertex 5. Edge 3 and edge 4, in this order, form a path between them with a total weight of 19, which is the minimum, so you should print 19.
- The third query changes the weight of edge 3 to 1.
- The fourth query asks you to print the distance between vertex 1 and vertex 5. Edge 3 and edge 4, in this order, form a path between them with a total weight of 1, which is the minimum, so you should print 11.
Sample 2 Input
7
1 2 1000000000
2 3 1000000000
3 4 1000000000
4 5 1000000000
5 6 1000000000
6 7 1000000000
3
2 1 6
1 1 294967296
2 1 6
Sample 2 Output
5000000000
4294967296
Sample 3 Input
1
1
2 1 1
Sample 3 Output
0
8
1 2 105
1 3 103
2 4 105
2 5 100
5 6 101
3 7 106
3 8 100
18
2 2 8
2 3 6
1 4 108
2 3 4
2 3 5
2 5 5
2 3 1
2 4 3
1 1 107
2 3 1
2 7 6
2 3 8
2 1 5
2 7 6
2 4 7
2 1 7
2 5 3
2 8 6
308
409
313
316
0
103
313
103
525
100
215
525
421
209
318
519