### Problem Statement

We have a grid with $2$ rows and $L$ columns. Let $(i,j)$ denote the square at the $i$-th row from the top $(i\in\lbrace1,2\rbrace)$ and $j$-th column from the left $(1\leq j\leq L)$. $(i,j)$ has an integer $x _ {i,j}$ written on it.

Find the number of integers $j$ such that $x _ {1,j}=x _ {2,j}$.

Here, the description of $x _ {i,j}$ is given to you as the run-length compressions of $(x _ {1,1},x _ {1,2},\ldots,x _ {1,L})$ and $(x _ {2,1},x _ {2,2},\ldots,x _ {2,L})$ into sequences of lengths $N _ 1$ and $N _ 2$, respectively: $((v _ {1,1},l _ {1,1}),\ldots,(v _ {1,N _ 1},l _ {1,N _ 1}))$ and $((v _ {2,1},l _ {2,1}),\ldots,(v _ {2,N _ 2},l _ {2,N _ 2}))$.

Here, the run-length compression of a sequence $A$ is a sequence of pairs $(v _ i,l _ i)$ of an element $v _ i$ of $A$ and a positive integer $l _ i$ obtained as follows.

1.  Split $A$ between each pair of different adjacent elements.
2.  For each sequence $B _ 1,B _ 2,\ldots,B _ k$ after the split, let $v _ i$ be the element of $B _ i$ and $l _ i$ be the length of $B _ i$.

### Input

The input is given from Standard Input in the following format:

```
$L$ $N _ 1$ $N _ 2$
$v _ {1,1}$ $l _ {1,1}$
$v _ {1,2}$ $l _ {1,2}$
$\vdots$
$v _ {1,N _ 1}$ $l _ {1,N _ 1}$
$v _ {2,1}$ $l _ {2,1}$
$v _ {2,2}$ $l _ {2,2}$
$\vdots$
$v _ {2,N _ 2}$ $l _ {2,N _ 2}$
```

### Output

Print a single line containing the answer.

### Constraints

-   $1\leq L\leq 10 ^ {12}$
-   $1\leq N _ 1,N _ 2\leq 10 ^ 5$
-   $1\leq v _ {i,j}\leq 10 ^ 9\ (i\in\lbrace1,2\rbrace,1\leq j\leq N _ i)$
-   $1\leq l _ {i,j}\leq L\ (i\in\lbrace1,2\rbrace,1\leq j\leq N _ i)$
-   $v _ {i,j}\neq v _ {i,j+1}\ (i\in\lbrace1,2\rbrace,1\leq j\lt N _ i)$
-   $l _ {i,1}+l _ {i,2}+\cdots+l _ {i,N _ i}=L\ (i\in\lbrace1,2\rbrace)$
-   All values in the input are integers.

4

The grid is shown below.

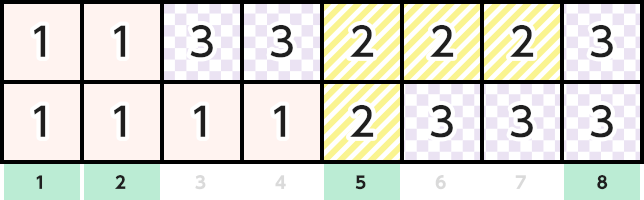
We have four integers j such that $x_{1,j}=x_{2,j}: j=1,2,5,8$. Thus, you should print 4.