9256: CF1817 - B. Fish Graph
[Creator : ]
Description
You are given a simple undirected graph with $n$ nodes and $m$ edges. Note that the graph is not necessarily connected. The nodes are labeled from $1$ to $n$.
We define a graph to be a Fish Graph if it contains a simple cycle with a special node $u$ belonging to the cycle. Apart from the edges in the cycle, the graph should have exactly $2$ extra edges. Both edges should connect to node $u$, but they should not be connected to any other node of the cycle.
Determine if the graph contains a subgraph that is a Fish Graph, and if so, find any such subgraph.
In this problem, we define a subgraph as a graph obtained by taking any subset of the edges of the original graph.
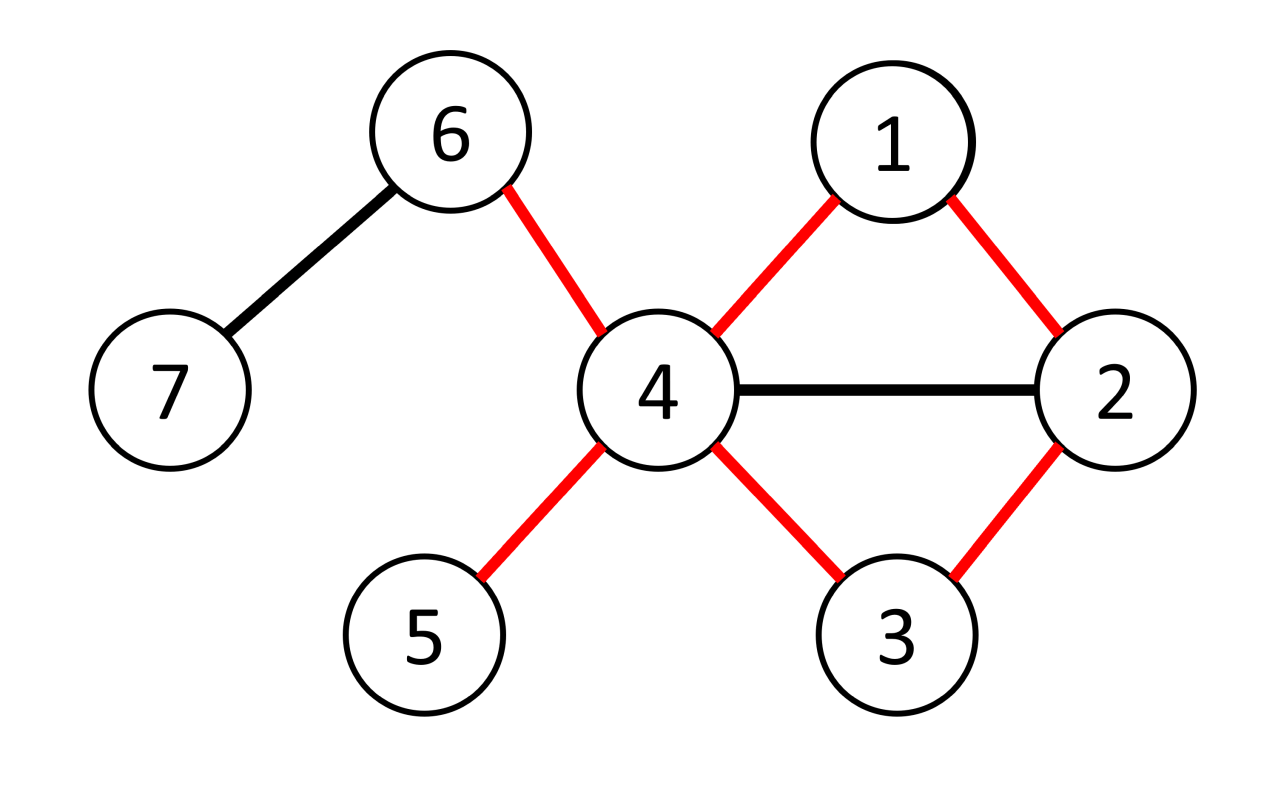
We define a graph to be a Fish Graph if it contains a simple cycle with a special node $u$ belonging to the cycle. Apart from the edges in the cycle, the graph should have exactly $2$ extra edges. Both edges should connect to node $u$, but they should not be connected to any other node of the cycle.
Determine if the graph contains a subgraph that is a Fish Graph, and if so, find any such subgraph.
In this problem, we define a subgraph as a graph obtained by taking any subset of the edges of the original graph.

Input
The first line of input contains the integer $t\ (1≤t≤1000)$, the number of test cases. The description of test cases follows.
The first line of each test case contains two integers, $n, m\ (1≤n,m≤2000)$ — the number of nodes and the number of edges.
Each of the next $m$ lines contains the description of an edge. Each line contains two integers $u_i, v_i\ (1≤u_i,v_i≤n,\ u_i≠v_i)$ — an edge connects node $u_i$ to node $v_i$.
It is guaranteed that no two edges connect the same unordered pair of nodes.
Furthermore, it is guaranteed that the sum of $n$ and the sum of $m$ over all test cases both do not exceed $2000$.
The first line of each test case contains two integers, $n, m\ (1≤n,m≤2000)$ — the number of nodes and the number of edges.
Each of the next $m$ lines contains the desc
It is guaranteed that no two edges connect the same unordered pair of nodes.
Furthermore, it is guaranteed that the sum of $n$ and the sum of $m$ over all test cases both do not exceed $2000$.
Output
For each testcase, output "YES" if the graph contains a subgraph that is a Fish Graph, otherwise print "NO". If the answer is "YES", on the following lines output a description of the subgraph.
The first line of the description contains one integer $k$ — the number of edges of the subgraph.
On the next $k$ lines, output the edges of the chosen subgraph. Each of the $k$ lines should contains two integers $u$ and $v\ (1≤u,v≤n,\ u≠v)$ — the edge between $u$ and $v$ belongs to the subgraph. The order in which $u$ and $v$ are printed does not matter, as long as the two nodes are connected by an edge in the original graph. The order in which you print the edges does not matter, as long as the resulting subgraph is a fish graph.
If there are multiple solutions, print any.
The first line of the desc
On the next $k$ lines, output the edges of the chosen subgraph. Each of the $k$ lines should contains two integers $u$ and $v\ (1≤u,v≤n,\ u≠v)$ — the edge between $u$ and $v$ belongs to the subgraph. The order in which $u$ and $v$ are printed does not matter, as long as the two nodes are connected by an edge in the original graph. The order in which you print the edges does not matter, as long as the resulting subgraph is a fish graph.
If there are multiple solutions, print any.
Sample 1 Input
3
7 8
1 2
2 3
3 4
4 1
4 5
4 6
4 2
6 7
7 7
6 7
1 2
2 3
3 4
4 1
1 3
3 5
4 4
1 3
3 4
4 1
1 2
Sample 1 Output
YES
6
5 4
6 4
4 3
1 4
2 1
3 2
YES
5
5 3
2 3
3 1
4 3
1 4
NO
In the first example, a possible valid subgraph contains the cycle 1→2→3→4→1. The special node of this cycle is node 4. The two extra edges 4−5 and 4−6 are both connected to 4, completing the Fish Graph.
In the second example, a possible valid subgraph contains the cycle 1→3→4→1. The special node of this cycle is node 3. The two extra edges 3−2 and 3−5 are both connected to 3, completing the Fish Graph.
In the last example, it can be proven that there is no valid subgraph.
In the second example, a possible valid subgraph contains the cycle 1→3→4→1. The special node of this cycle is node 3. The two extra edges 3−2 and 3−5 are both connected to 3, completing the Fish Graph.
In the last example, it can be proven that there is no valid subgraph.