9237: ABC291 —— Ex - Balanced Tree
[Creator : ]
Description
### Problem Statement
You are given a tree $T$ with $N$ vertices. The $i$-th edge connects vertices $A_i$ and $B_i$.
Construct an $N$-vertex rooted tree $R$ that satisfies the following conditions.
- For all integer pairs $(x,y)$ such that $1 \leq x < y \leq N$,
- if the lowest common ancestor in $R$ of vertices $x$ and $y$ is vertex $z$, then vertex $z$ in $T$ is on the simple path between vertices $x$ and $y$.
- In $R$, for all vertices $v$ except for the root, the number of vertices of the subtree rooted at $v$, multiplied by $2$, does not exceed the number of vertices of the subtree rooted at the parent of $v$.
We can prove that such a rooted tree always exists.
You are given a tree $T$ with $N$ vertices. The $i$-th edge connects vertices $A_i$ and $B_i$.
Construct an $N$-vertex rooted tree $R$ that satisfies the following conditions.
- For all integer pairs $(x,y)$ such that $1 \leq x < y \leq N$,
- if the lowest common ancestor in $R$ of vertices $x$ and $y$ is vertex $z$, then vertex $z$ in $T$ is on the simple path between vertices $x$ and $y$.
- In $R$, for all vertices $v$ except for the root, the number of vertices of the subtree rooted at $v$, multiplied by $2$, does not exceed the number of vertices of the subtree rooted at the parent of $v$.
We can prove that such a rooted tree always exists.
Input
### Input
The input is given from Standard Input in the following format:
```
$N$
$A_1$ $B_1$
$\vdots$
$A_{N-1}$ $B_{N-1}$
```
The input is given from Standard Input in the following format:
```
$N$
$A_1$ $B_1$
$\vdots$
$A_{N-1}$ $B_{N-1}$
```
Output
### Output
Let $R$ be a rooted tree that satisfies the conditions in the Problem Statement. Suppose that the parent of vertex $i$ in $R$ is vertex $p_i$. (If $i$ is the root, let $p_i=-1$.)
Print $N$ integers $p_1,\ldots,p_N$, with spaces in between.
Let $R$ be a rooted tree that satisfies the conditions in the Problem Statement. Suppose that the parent of vertex $i$ in $R$ is vertex $p_i$. (If $i$ is the root, let $p_i=-1$.)
Print $N$ integers $p_1,\ldots,p_N$, with spaces in between.
Constraints
### Constraints
- $1 \leq N \leq 10^5$
- $1\leq A_i,B_i \leq N$
- All values in the input are integers.
- The given graph is a tree.
- $1 \leq N \leq 10^5$
- $1\leq A_i,B_i \leq N$
- All values in the input are integers.
- The given graph is a tree.
Sample 1 Input
4
1 2
2 3
3 4
Sample 1 Output
2 -1 4 2
For example, the lowest common ancestor in R of vertices 1 and 3 is vertex 2; in T, vertex 2 is on the simple path between vertices 1 and 3.
Also, for example, in R, the subtree rooted at vertex 4 has two vertices, and the number multiplied by two does not exceed the number of vertices of the subtree rooted at vertex 2, which has 4 vertices.
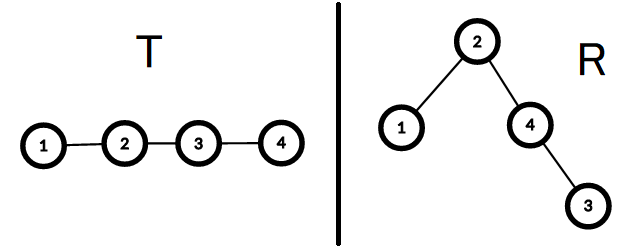
Also, for example, in R, the subtree rooted at vertex 4 has two vertices, and the number multiplied by two does not exceed the number of vertices of the subtree rooted at vertex 2, which has 4 vertices.

Sample 2 Input
5
1 2
1 3
1 4
1 5
Sample 2 Output
-1 1 1 1 1