9219: ABC289 —— F - Teleporter Takahashi
[Creator : ]
Description
### Problem Statement
Takahashi is on an $xy$-plane. Initially, he is at point $(s _ x,s _ y)$, and he wants to reach point $(t _ x,t _ y)$.
On the $xy$-plane is a rectangle $R=\lbrace(x,y)\mid a-0.5\leq x\leq b+0.5,c-0.5\leq y\leq d+0.5\rbrace$. Consider the following operation:
- Choose a lattice point $(x,y)$ contained in the rectangle $R$. Takahashi teleports to the point symmetric to his current position with respect to point $(x,y)$.
Determine if he can reach point $(t _ x,t _ y)$ after repeating the operation above between $0$ and $10^6$ times, inclusive. If it is possible, construct a sequence of operations that leads him to point $(t _ x,t _ y)$.
Takahashi is on an $xy$-plane. Initially, he is at point $(s _ x,s _ y)$, and he wants to reach point $(t _ x,t _ y)$.
On the $xy$-plane is a rectangle $R=\lbrace(x,y)\mid a-0.5\leq x\leq b+0.5,c-0.5\leq y\leq d+0.5\rbrace$. Consider the following operation:
- Choose a lattice point $(x,y)$ contained in the rectangle $R$. Takahashi teleports to the point symmetric to his current position with respect to point $(x,y)$.
Determine if he can reach point $(t _ x,t _ y)$ after repeating the operation above between $0$ and $10^6$ times, inclusive. If it is possible, construct a sequence of operations that leads him to point $(t _ x,t _ y)$.
Input
### Input
The input is given from Standard Input in the following format:
```
$s _ x$ $s _ y$
$t _ x$ $t _ y$
$a$ $b$ $c$ $d$
```
The input is given from Standard Input in the following format:
```
$s _ x$ $s _ y$
$t _ x$ $t _ y$
$a$ $b$ $c$ $d$
```
Output
### Output
In the first line, print `Yes` if Takahashi can reach point $(t _ x,t _ y)$ after repeating the operation between $0$ and $10^6$ times, inclusive, and `No` otherwise. If and only if you print `Yes` in the first line, print $d$ more lines, where $d$ is the length of the sequence of operations you have constructed ($d$ must satisfy $0\leq d\leq10^6$). The $(1+i)$-th line $(1\leq i\leq d)$ should contain the space-separated coordinates of the point $(x, y)\in R$, in this order, that is chosen in the $i$-th operation.
In the first line, print `Yes` if Takahashi can reach point $(t _ x,t _ y)$ after repeating the operation between $0$ and $10^6$ times, inclusive, and `No` otherwise. If and only if you print `Yes` in the first line, print $d$ more lines, where $d$ is the length of the sequence of operations you have constructed ($d$ must satisfy $0\leq d\leq10^6$). The $(1+i)$-th line $(1\leq i\leq d)$ should contain the space-separated coordinates of the point $(x, y)\in R$, in this order, that is chosen in the $i$-th operation.
Constraints
### Constraints
- $0\leq s _ x,s _ y,t _ x,t _ y\leq2\times10^5$
- $0\leq a\leq b\leq2\times10^5$
- $0\leq c\leq d\leq2\times10^5$
- All values in the input are integers.
- $0\leq s _ x,s _ y,t _ x,t _ y\leq2\times10^5$
- $0\leq a\leq b\leq2\times10^5$
- $0\leq c\leq d\leq2\times10^5$
- All values in the input are integers.
Sample 1 Input
1 2
7 8
7 9 0 3
Sample 1 Output
Yes
7 0
9 3
7 1
8 1
For example, the following choices lead him from (1,2) to (7,8).
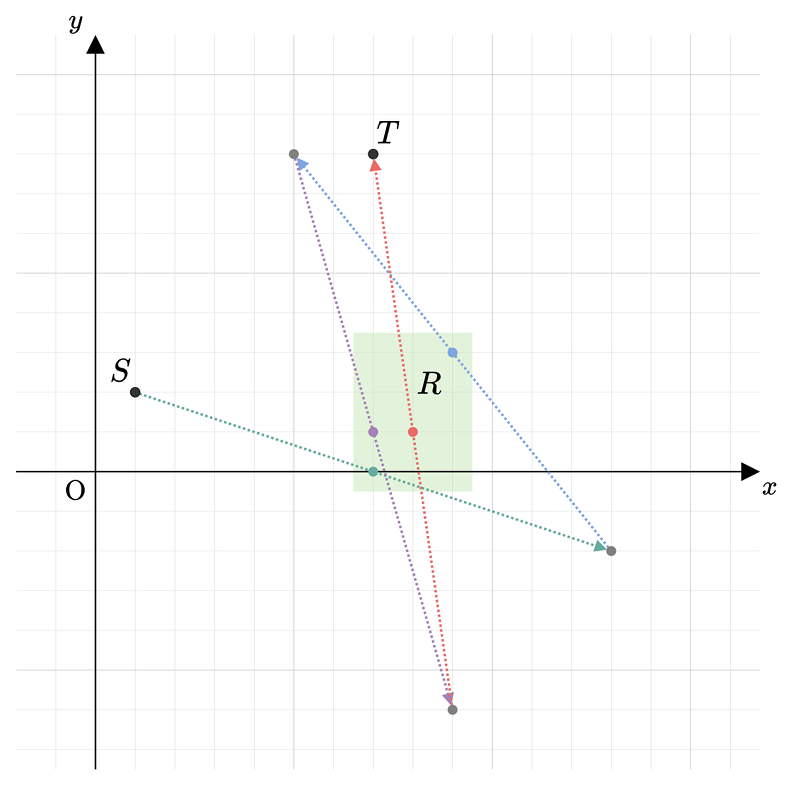
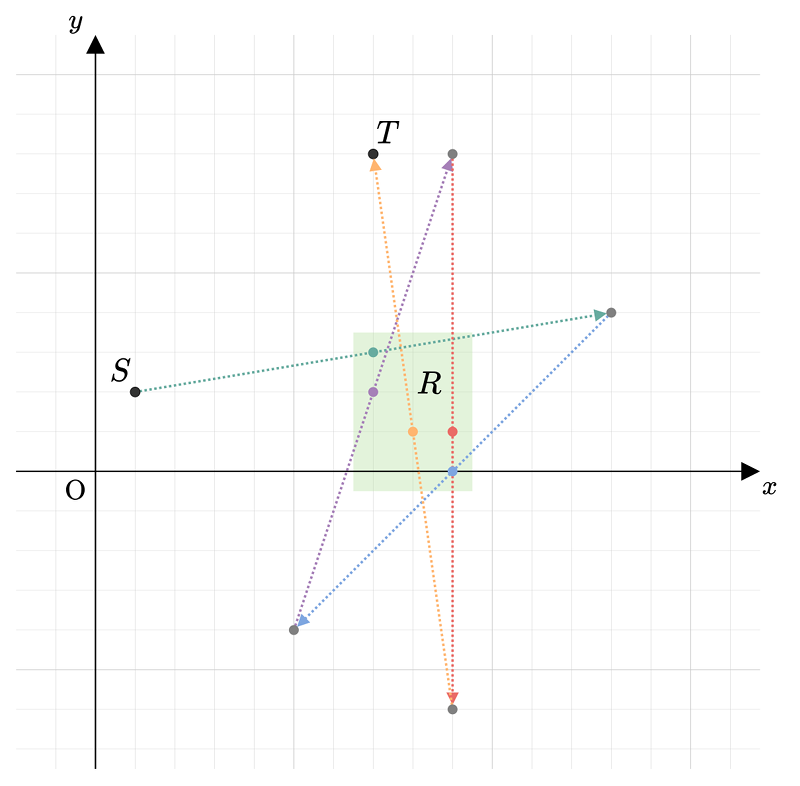
Any output that satisfies the conditions is accepted; for example, printing
is also accepted.
- Choose (7,0). Takahashi moves to (13,−2).
- Choose (9,3). Takahashi moves to (5,8).
- Choose (7,1). Takahashi moves to (9,−6).
- Choose (8,1). Takahashi moves to (7,8).

Any output that satisfies the conditions is accepted; for example, printing
Yes 7 3 9 0 7 2 9 1 8 1
is also accepted.

Sample 2 Input
0 0
8 4
5 5 0 0
Sample 2 Output
No
No sequence of operations leads him to point (8,4).

Sample 3 Input
1 4
1 4
100 200 300 400
Sample 3 Output
Yes
Takahashi may already be at the destination in the beginning.
22 2
16 7
14 30 11 14
No