9215: ABC289 —— B - V
[Creator : ]
Description
### Problem Statement
There are $N$ integers from $1$ through $N$ arranged in a line in ascending order.
Between them are $M$ "レ" marks. The $i$-th "レ" mark is between the integer $a_i$ and integer $(a_i + 1)$.
You read each of the $N$ integers once by the following procedure.
- Consider an undirected graph $G$ with $N$ vertices numbered $1$ through $N$ and $M$ edges. The $i$-th edge connects vertex $a_i$ and vertex $(a_i+1)$.
- Repeat the following operation until there is no unread integer:
- let $x$ be the minimum unread integer. Choose the connected component $C$ containing vertex $x$, and read all the numbers of the vertices contained in $C$ in descending order.
For example, suppose that integers and "レ" marks are arranged in the following order:
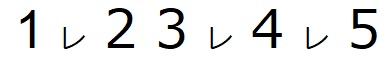
(In this case, $N = 5, M = 3$, and $a = (1, 3, 4)$.)
Then, the order to read the integers is determined to be $2, 1, 5, 4$, and $3$, as follows:
- At first, the minimum unread integer is $1$, and the connected component of $G$ containing vertex $1$ has vertices $\lbrace 1, 2 \rbrace$, so $2$ and $1$ are read in this order.
- Then, the minimum unread integer is $3$, and the connected component of $G$ containing vertex $3$ has vertices $\lbrace 3, 4, 5 \rbrace$, so $5$, $4$, and $3$ are read in this order.
- Now that all integers are read, terminate the procedure.
Given $N, M$, and $(a_1, a_2, \dots, a_M)$, print the order to read the $N$ integers.
What is a connected component? A subgraph of a graph is a graph obtained by choosing some vertices and edges from the original graph.
A graph is said to be connected if and only if one can travel between any two vertices in the graph via edges.
A connected component is a connected subgraph that is not contained in any larger connected subgraph.
There are $N$ integers from $1$ through $N$ arranged in a line in ascending order.
Between them are $M$ "レ" marks. The $i$-th "レ" mark is between the integer $a_i$ and integer $(a_i + 1)$.
You read each of the $N$ integers once by the following procedure.
- Consider an undirected graph $G$ with $N$ vertices numbered $1$ through $N$ and $M$ edges. The $i$-th edge connects vertex $a_i$ and vertex $(a_i+1)$.
- Repeat the following operation until there is no unread integer:
- let $x$ be the minimum unread integer. Choose the connected component $C$ containing vertex $x$, and read all the numbers of the vertices contained in $C$ in descending order.
For example, suppose that integers and "レ" marks are arranged in the following order:
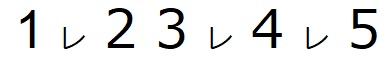
(In this case, $N = 5, M = 3$, and $a = (1, 3, 4)$.)
Then, the order to read the integers is determined to be $2, 1, 5, 4$, and $3$, as follows:
- At first, the minimum unread integer is $1$, and the connected component of $G$ containing vertex $1$ has vertices $\lbrace 1, 2 \rbrace$, so $2$ and $1$ are read in this order.
- Then, the minimum unread integer is $3$, and the connected component of $G$ containing vertex $3$ has vertices $\lbrace 3, 4, 5 \rbrace$, so $5$, $4$, and $3$ are read in this order.
- Now that all integers are read, terminate the procedure.
Given $N, M$, and $(a_1, a_2, \dots, a_M)$, print the order to read the $N$ integers.
What is a connected component? A subgraph of a graph is a graph obtained by choosing some vertices and edges from the original graph.
A graph is said to be connected if and only if one can travel between any two vertices in the graph via edges.
A connected component is a connected subgraph that is not contained in any larger connected subgraph.
Input
### Input
The input is given from Standard Input in the following format:
```
$N$ $M$
$a_1$ $a_2$ $\dots$ $a_M$
```
The input is given from Standard Input in the following format:
```
$N$ $M$
$a_1$ $a_2$ $\dots$ $a_M$
```
Output
### Output
Print the answer in the following format, where $p_i$ is the $i$-th integers to read.
```
$p_1$ $p_2$ $\dots$ $p_N$
```
Print the answer in the following format, where $p_i$ is the $i$-th integers to read.
```
$p_1$ $p_2$ $\dots$ $p_N$
```
Constraints
### Constraints
- $1 \leq N \leq 100$
- $0 \leq M \leq N - 1$
- $1 \leq a_1 \lt a_2 \lt \dots \lt a_M \leq N-1$
- All values in the input are integers.
- $1 \leq N \leq 100$
- $0 \leq M \leq N - 1$
- $1 \leq a_1 \lt a_2 \lt \dots \lt a_M \leq N-1$
- All values in the input are integers.
Sample 1 Input
5 3
1 3 4
Sample 1 Output
2 1 5 4 3
As described in the Problem Statement, if integers and "レ" marks are arranged in the following order:
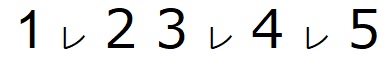
then the integers are read in the following order: 2,1,5,4, and 3.
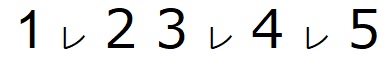
then the integers are read in the following order: 2,1,5,4, and 3.
Sample 2 Input
5 0
Sample 2 Output
1 2 3 4 5
There may be no "レ" mark.
Sample 3 Input
10 6
1 2 3 7 8 9
Sample 3 Output
4 3 2 1 5 6 10 9 8 7