### Problem Statement

You are given a simple undirected graph with $N$ vertices and $M$ edges. The vertices are numbered $1, 2, \dots, N$, and the edges are numbered $1, 2, \dots, M$.  
Edge $i \, (i = 1, 2, \dots, M)$ connects vertices $u_i$ and $v_i$.

Determine if this graph is a path graph.

What is a simple undirected graph? A **simple undirected graph** is a graph without self-loops or multiple edges whose edges do not have a direction.

What is a path graph? A graph with $N$ vertices numbered $1, 2, \dots, N$ is said to be a **path graph** if and only if there is a sequence $(v_1, v_2, \dots, v_N)$ that is a permutation of $(1, 2, \dots, N)$ and satisfies the following conditions:

-   For all $i = 1, 2, \dots, N-1$, there is an edge connecting vertices $v_i$ and $v_{i+1}$.
-   If integers $i$ and $j$ satisfies $1 \leq i, j \leq N$ and $|i - j| \geq 2$, then there is no edge that connects vertices $v_i$ and $v_j$.

### Input

The input is given from Standard Input in the following format:

```
$N$ $M$
$u_1$ $v_1$
$u_2$ $v_2$
$\vdots$
$u_M$ $v_M$
```

### Output

Print `Yes` if the given graph is a path graph; print `No` otherwise.

### Constraints

-   $2 \leq N \leq 2 \times 10^5$
-   $0 \leq M \leq 2 \times 10^5$
-   $1 \leq u_i, v_i \leq N \, (i = 1, 2, \dots, M)$
-   All values in the input are integers.
-   The graph given in the input is simple.

Yes

Illustrated below is the given graph, which is a path graph.

No

Illustrated below is the given graph, which is not a path graph.

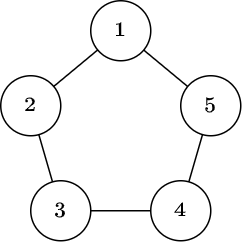
No

Illustrated below is the given graph, which is not a path graph.