9196: ABC285 —— G - Tatami
[Creator : ]
Description
We have a grid with $H$ horizontal rows and $W$ vertical columns. We denote by square $(i,j)$ the square at the $i$-th row from the top and $j$-th column from the left.
We want to cover this grid with $1 \times 1$ tiles and $1 \times 2$ tiles so that no tiles overlap and everywhere is covered by a tile. (A tile can be rotated.)
Each square has `1`, `2`, or `?` written on it. The character written on square $(i, j)$ is $c_{i,j}$.
A square with `1` written on it must be covered by a $1 \times 1$ tile, and a square with `2` by a $1 \times 2$ tile. A square with `?` may be covered by any kind of tile.
Determine if there is such a placement of tiles.
We want to cover this grid with $1 \times 1$ tiles and $1 \times 2$ tiles so that no tiles overlap and everywhere is covered by a tile. (A tile can be rotated.)
Each square has `1`, `2`, or `?` written on it. The character written on square $(i, j)$ is $c_{i,j}$.
A square with `1` written on it must be covered by a $1 \times 1$ tile, and a square with `2` by a $1 \times 2$ tile. A square with `?` may be covered by any kind of tile.
Determine if there is such a placement of tiles.
Input
The input is given from Standard Input in the following format:
```
$H$ $W$
$c_{1,1}c_{1,2}\ldots c_{1,W}$
$\vdots$
$c_{H,1}c_{H,2}\ldots c_{H,W}$
```
```
$H$ $W$
$c_{1,1}c_{1,2}\ldots c_{1,W}$
$\vdots$
$c_{H,1}c_{H,2}\ldots c_{H,W}$
```
Output
Print `Yes` if there is a placement of tiles to satisfy the conditions in the Problem Statement; print `No` otherwise.
Constraints
- $1 \leq H,W \leq 300$
- $H$ and $W$ are integers.
- $c_{i,j}$ is one of `1`, `2`, and `?`.
- $H$ and $W$ are integers.
- $c_{i,j}$ is one of `1`, `2`, and `?`.
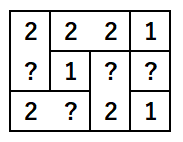
Sample 1 Input
3 4
2221
?1??
2?21
Sample 1 Output
Yes
For example, the following placement satisfies the conditions.

Sample 2 Input
3 4
2?21
??1?
2?21
Sample 2 Output
No
There is no placement that satisfies the conditions.
Sample 3 Input
5 5
11111
11111
11211
11111
11111
Sample 3 Output
No