You are to generate a graph by the following procedure.

-   Choose a simple undirected graph with $N$ unlabeled vertices.
-   Write a positive integer at most $K$ in each vertex in the graph. Here, there must not be a positive integer at most $K$ that is not written in any vertex.

Find the number of possible graphs that can be obtained, modulo $P$. ($P$ is a prime.)

Two graphs are considered the same if and only if one can label the vertices in each graph as $v_1, v_2, \dots, v_N$ to satisfy the following conditions.

-   For every $i$ such that $1 \leq i \leq N$, the numbers written in vertex $v_i$ in the two graphs are the same.
-   For every $i$ and $j$ such that $1 \leq i \lt j \leq N$, there is an edge between $v_i$ and $v_j$ in one of the graphs if and only if there is an edge between $v_i$ and $v_j$ in the other graph.

The input is given from Standard Input in the following format:

```
$N$ $K$ $P$
```

Print the answer.

-   $1 \leq K \leq N \leq 30$
-   $10^8 \leq P \leq 10^9$
-   $P$ is a prime.
-   All values in the input are integers.

4

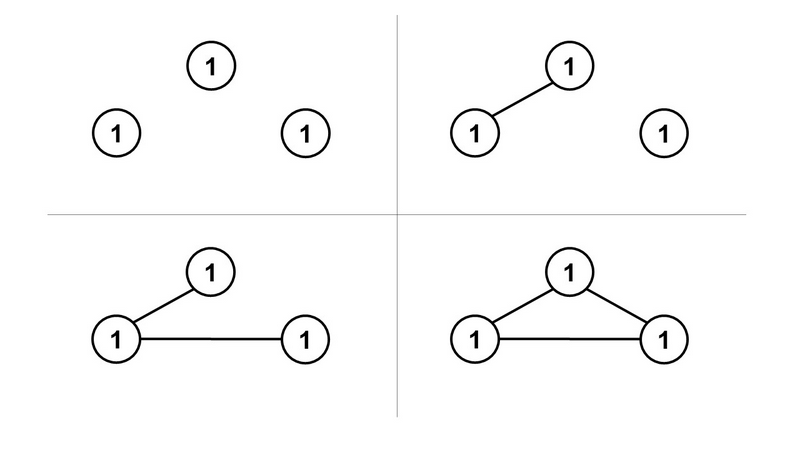
The following four graphs satisfy the condition.

12

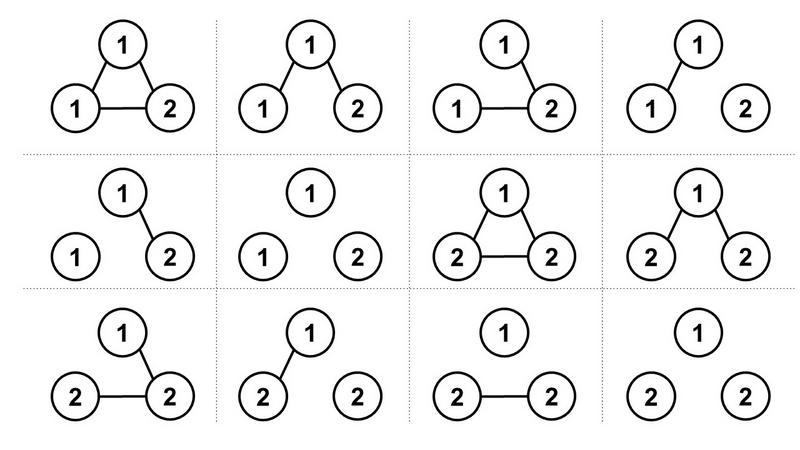
The following 12 graphs satisfy the condition.