You are given a simple undirected graph with $N$ vertices numbered $1$ to $N$ and $M$ edges numbered $1$ to $M$. Edge $i$ connects vertex $u_i$ and vertex $v_i$.  
Find the number of connected components in this graph.

Notes

A simple undirected graph is a graph that is simple and has undirected edges.  
A graph is simple if and only if it has no self-loop or multi-edge.
A subgraph of a graph is a graph formed from some of the vertices and edges of that graph.  
A graph is connected if and only if one can travel between every pair of vertices via edges.  
A connected component is a connected subgraph that is not part of any larger connected subgraph.

The input is given from Standard Input in the following format:

```
$N$ $M$
$u_1$ $v_1$
$u_2$ $v_2$
$\vdots$
$u_M$ $v_M$
```

Print the answer.

-   $1 \leq N \leq 100$
-   $0 \leq M \leq \frac{N(N - 1)}{2}$
-   $1 \leq u_i, v_i \leq N$
-   The given graph is simple.
-   All values in the input are integers.

2

The given graph contains the following two connected components:

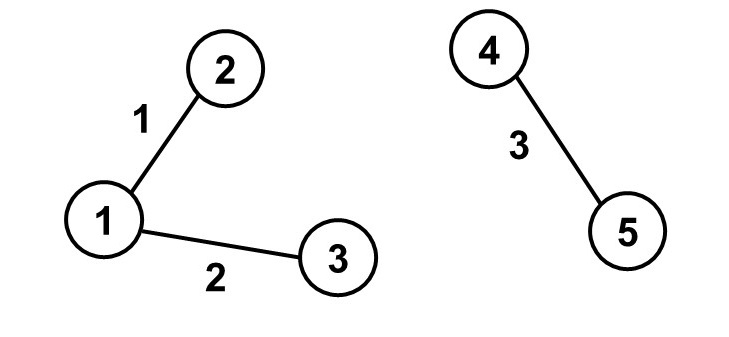
• a subgraph formed from vertices 1, 2, 3, and edges 1, 2;
• a subgraph formed from vertices 4, 5, and edge 3.