This is an interactive task, where your and the judge's programs interact via Standard Input and Output.

You and the judge will follow the procedure below. The procedure consists of phases $1$ and $2$; phase $1$ is immediately followed by phase $2$.

(Phase $1$)

-   The judge gives you an integer $N$.
-   You print an integer $M$ between $1$ and $50000$, inclusive.
-   You also print $M$ pairs of integers $(l_1, r_1), (l_2, r_2), \ldots, (l_M, r_M)$ such that $1 \leq l_i \leq r_i \leq N$ for every $i = 1, 2, \ldots, M$ (the $M$ pairs do not have to be distinct).

(Phase $2$)

-   The judge gives you an integer $Q$.
-   You and the judge repeats the following $Q$ times.
    -   The judge gives you two integers $L$ and $R$ as a query.
    -   You respond with two integers $a$ and $b$ between $1$ and $M$, inclusive (possibly with $a = b$). Here, $a$ and $b$ must satisfy the condition below. Otherwise, your submission will be judged incorrect.
        -   The union of the set $\lbrace l_a, l_a+1, \ldots, r_a\rbrace$ and the set $\lbrace l_b, l_b+1, \ldots, r_b\rbrace$ equals the set $\lbrace L, L+1, \ldots, R\rbrace$.

After the procedure above, terminate the program immediately to be judged correct.

This is an interactive task, where your and the judge's programs interact via Standard Input and Output.

(Phase $1$)

-   First, $N$ is given from the input.
-   Next, an integer $M$ between $1$ and $50000$, inclusive, should be printed.
-   Then, $(l_1, r_1), (l_2, r_2), \ldots, (l_M, r_M)$ should be printed, one at a time. Specifically, for each $i = 1, 2, \ldots, M$, the $i$-th output should be $(l_i, r_i)$ in the following format:

```
$l_i$ $r_i$
```

(Phase $2$)

-   First, $Q$ is given from the input.
-   In each query, integers $L$ and $R$ representing the query are given in the following format:

```
$L$ $R$
```

-   In response to each query, two integers $a$ and $b$ should be printed in the following format:

```
$a$ $b$

```

Cautions

-   At the end of each output, print a newline and flush Standard Output. Otherwise, you may get the TLE verdict.
-   If your program prints a malformed output or quits prematurely, the verdict will be indeterminate. Particularly, note that in case of a runtime error, the verdict may be WA or TLE instead of RE.
-   After phase $2$, immediately terminate the program. Otherwise, the verdict will be indeterminate.
-   $L$ and $R$ given in phase $2$ will be decided according to $(l_1, r_1), (l_2, r_2), \ldots, (l_M, r_M)$ you print in phase $1$.

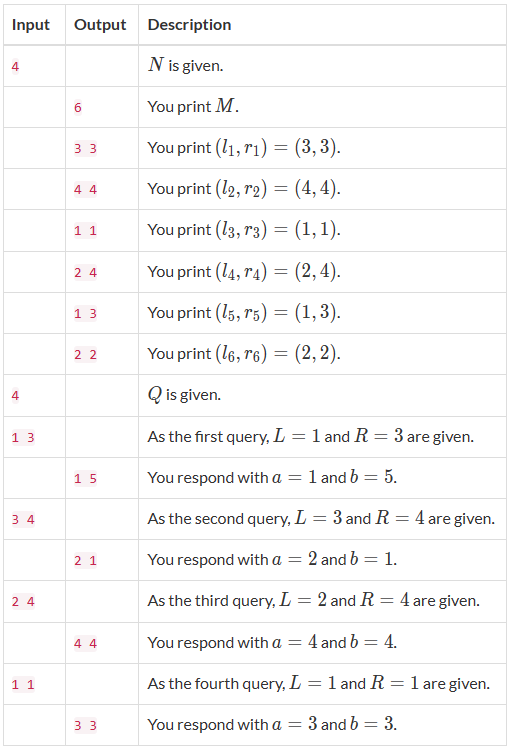
Below is a sample interaction with $N = 4$ and $Q = 4$.

-   $1 \leq N \leq 4000$
-   $1 \leq Q \leq 10^5$
-   $1 \leq L \leq R \leq N$
-   All values in the input are integers.