9136: ABC331 —— D - Tile Pattern
[Creator : ]
Description
There is a grid with $10^9$ by $10^9$ squares. Let $(i, j)$ denote the square at the $(i + 1)$-th row from the top and the $(j + 1)$-th column from the left $(0 \leq i, j \lt 10^9)$. (Note the unusual index assignment.)
Each square is black or white. The color of the square $(i, j)$ is represented by a character $P[i \bmod N][j \bmod N]$, where `B` means black, and `W` means white. Here, $a \bmod b$ denotes the remainder when $a$ is divided by $b$.
Answer $Q$ queries.
Each query gives you four integers $A, B, C, D$ and asks you to find the number of black squares contained in the rectangular area with $(A, B)$ as the top-left corner and $(C, D)$ as the bottom-right corner.
Each square is black or white. The color of the square $(i, j)$ is represented by a character $P[i \bmod N][j \bmod N]$, where `B` means black, and `W` means white. Here, $a \bmod b$ denotes the remainder when $a$ is divided by $b$.
Answer $Q$ queries.
Each query gives you four integers $A, B, C, D$ and asks you to find the number of black squares contained in the rectangular area with $(A, B)$ as the top-left corner and $(C, D)$ as the bottom-right corner.
Input
The input is given from Standard Input in the following format. Here, $\text{query}_i$ is the $i$\-th query to be processed.
```
$N$ $Q$
$P[0][0]P[0][1]\dots P[0][N-1]$
$P[1][0]P[1][1]\dots P[1][N-1]$
$\vdots$
$P[N-1][0]P[N-1][1]\dots P[N-1][N-1]$
$\text{query}_1$
$\text{query}_2$
$\vdots$
$\text{query}_Q$
```
Each query is given in the following format:
```
$A$ $B$ $C$ $D$
```
```
$N$ $Q$
$P[0][0]P[0][1]\dots P[0][N-1]$
$P[1][0]P[1][1]\dots P[1][N-1]$
$\vdots$
$P[N-1][0]P[N-1][1]\dots P[N-1][N-1]$
$\text{query}_1$
$\text{query}_2$
$\vdots$
$\text{query}_Q$
```
Each query is given in the following format:
```
$A$ $B$ $C$ $D$
```
Output
Follow the instructions in the problem statement and print the answers to the queries, separated by newlines.
Constraints
- $1 \leq N \leq 1000$
- $P[i][j]$ is `W` or `B`.
- $1 \leq Q \leq 2 \times 10^5$
- $0 \leq A \leq C \lt 10^9$
- $0 \leq B \leq D \lt 10^9$
- $N, Q, A, B, C, D$ are all integers.
- $P[i][j]$ is `W` or `B`.
- $1 \leq Q \leq 2 \times 10^5$
- $0 \leq A \leq C \lt 10^9$
- $0 \leq B \leq D \lt 10^9$
- $N, Q, A, B, C, D$ are all integers.
Sample 1 Input
3 2
WWB
BBW
WBW
1 2 3 4
0 3 4 5
Sample 1 Output
4
7
The figure below illustrates the upper left part of the grid.
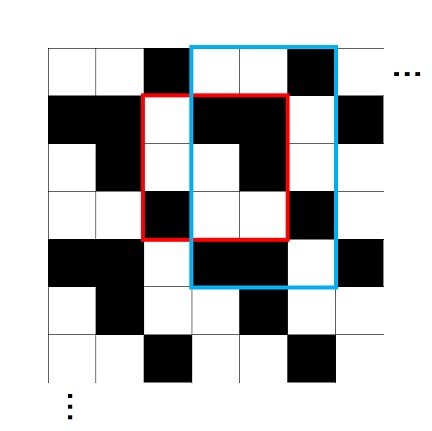
For the first query, the rectangular area with (1,2) as the top-left corner and (3,4) as the bottom-right corner, surrounded by the red frame in the figure, contains four black squares.
For the second query, the rectangular area with (0,3) as the top-left corner and (4,5) as the bottom-right corner, surrounded by the blue frame in the figure, contains seven black squares.

For the first query, the rectangular area with (1,2) as the top-left corner and (3,4) as the bottom-right corner, surrounded by the red frame in the figure, contains four black squares.
For the second query, the rectangular area with (0,3) as the top-left corner and (4,5) as the bottom-right corner, surrounded by the blue frame in the figure, contains seven black squares.
Sample 2 Input
10 5
BBBWWWBBBW
WWWWWBBBWB
BBBWBBWBBB
BBBWWBWWWW
WWWWBWBWBW
WBBWBWBBBB
WWBBBWWBWB
WBWBWWBBBB
WBWBWBBWWW
WWWBWWBWWB
5 21 21 93
35 35 70 43
55 72 61 84
36 33 46 95
0 0 999999999 999999999
Sample 2 Output
621
167
44
344
500000000000000000